JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)
DPL18 Count Partitions With Given Difference
Before the Moving on the Thsi Problem
Let's talk about the Edge Case that we Not Discuss in the DPL17
if in DPL17 Our Array Contains the 0 Values then Our Code Not Work Becouse we wrote the Code on the Bases of th Constrain that is num is: 1 <= 'n' <= 100
But if We put the 0 in the Array then this Gives Wrong Answer
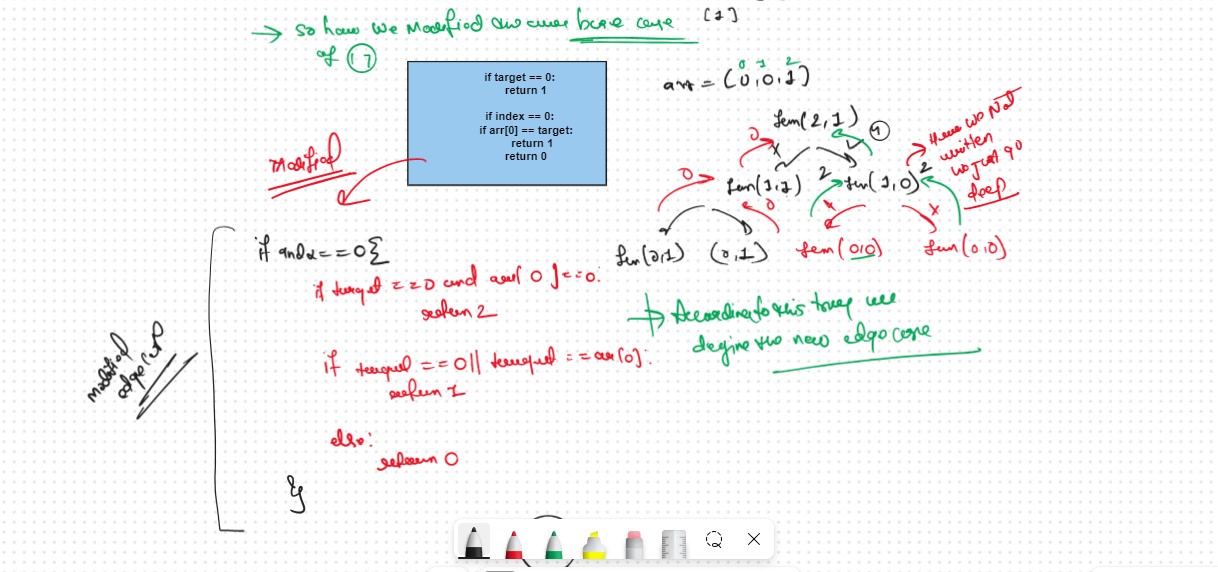
Let the target arr = [0,0,1] and the target = 1
The previous code will give us the answer 1 as it first takes the element arr[2] and then finds the answer by picking it. Then from the base condition, we will return 0 ( as the target will become 0 by picking 1). But for this question, the answer will be 4 with the following subsets({0,1},{0,1},{0,0,1} and {1}).
 Base Case Modification
First of all, we will remove target==0 because now when target == 0, there can be many 0s present in the array which needs to be counted in the answer.
Now, the following cases can arise when we are at index 0, if the target sum is 0 and the first index is also 0, like in case [0,1], we can form the subset in two ways, either by considering the first element or leaving it, so we can return 2.
Else at index 0, if target == 0, and the first element is not 0, it means we will not pick the first element so we just return 1 way.
Or if at index 0, when the first element is not 0, and the target is equal to the first element , then we will include it in the subset and we will return 1 way.
Else in all other cases, we simply return 0.
Base Case Modification
First of all, we will remove target==0 because now when target == 0, there can be many 0s present in the array which needs to be counted in the answer.
Now, the following cases can arise when we are at index 0, if the target sum is 0 and the first index is also 0, like in case [0,1], we can form the subset in two ways, either by considering the first element or leaving it, so we can return 2.
Else at index 0, if target == 0, and the first element is not 0, it means we will not pick the first element so we just return 1 way.
Or if at index 0, when the first element is not 0, and the target is equal to the first element , then we will include it in the subset and we will return 1 way.
Else in all other cases, we simply return 0.
 Final Modified Base Case is
Final Modified Base Case is
if(ind == 0){
if(target==0 && arr[0]==0)
return 2;
if(target==0 || target == arr[0])
return 1;
return 0;
}
Used this Base Case in the DPL17, For if Many 0 Include in the Array then We Want the Right Answer then Remember this Base Case.
We are given an array ‘ARR’ with N positive integers and an integer D. We need to count the number of ways we can partition the given array into two subsets, S1 and S2 such that S1 – S2 = D and S1 is always greater than or equal to S2.
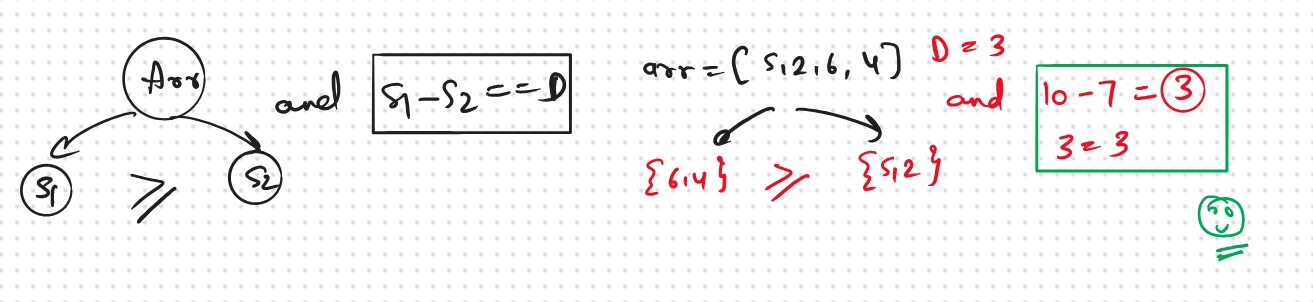
Again This question is a slight modification of the problem discussed in LDP15 & DP17. We need to partition the array(say S) into two subsets(say S1 and S2). According to the question:
We Just Changed the Slight Base Case in the DPL15 and Everything Will Be Same As From DPL15
Algorithm / Intuition
Sum of elements of S1 + sum of elements of S2 = sum of elements of S.
Sum of elements of S1 > sum of elements of S2.
If we calculate the total sum of elements of the array (say totSum), we can say that.
S1 = totSum – S2
Now solving for equations (i) and (iii), we can say that S2 = (totSum – D)/2
Edge Cases:
As the array elements are positive integers including zero, we don’t want to find the case when S2 is negative or we can say that totSum is lesser than D, therefore if totSum < D, we simply return 0.
S2 can’t be a fraction, as all elements are integers, therefore if totSum – D is odd, we can return 0.
Now remaining Entire 👇 Process will Be Same As Like in DPL15
what a Subsequence/Subset?
A subset/subsequence is a contiguous or non-contiguous part of an array, where elements appear in the same order as the original array.
For example, for the array: [2,3,1] , the subsequences will be [{2},{3},{1},{2,3},{2,1},{3,1},{2,3,1}] but {3,2} is not a subsequence because its elements are not in the same order as the original array.

In this Question first thing Comes into the My Mind is Generate all the Possible Subsecquance and check if any sum(subset) == k or not
I Have Two Option for this Question
Power Set Concept
Recursion Concept
But in this Problem we Just Required the Only One Subset no Need to Check All the Subsetst
thats why I go with the Recursion Approch
Recursice Approch
Steps to form the Recursive Solution
Step 1: Express the problem in terms of indexes.
The array will have an index but there is one more parameter “target”. We are given the initial problem to find whether there exists in the whole array a subsequence whose sum is equal to the target.
So, we can say that initially, we need to fun(n-1, target) which means that we need to find whether there exists a subsequence in the array from index 0 to n-1, whose sum is equal to the target. Similarly, we can generalize it for any index ind as follows:
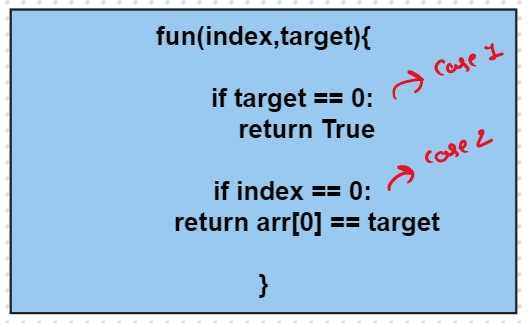
 Our Base
If target == 0, it means that we have already found the subsequence from the previous steps, so we can return true.
If ind==0, it means we are at the first element, so we need to return arr[ind]==target. If the element is equal to the target we return true else false.
Our Base
If target == 0, it means that we have already found the subsequence from the previous steps, so we can return true.
If ind==0, it means we are at the first element, so we need to return arr[ind]==target. If the element is equal to the target we return true else false.
The Recursive Function is
 Step 2: Try out all possible choices at a given index.
Step 2: Try out all possible choices at a given index.
We need to generate all the subsequences. We will use the pick/non-pick technique as discussed in, That we All Ready Learn in the Recursion Series.
We have two choices:
Exclude the current element in the subsequence: We first try to find a subsequence without considering the current index element. For this, we will make a recursive call to f(ind-1,target).
Include the current element in the subsequence: We will try to find a subsequence by considering the current index as element as part of subsequence. As we have included arr[ind], the updated target which we need to find in the rest if the array will be target – arr[ind]. Therefore, we will call f(ind-1,target-arr[ind]).
Note: We will consider the current element in the subsequence only when the current element is less or equal to the target.

Step 3: Return (taken || notTaken)
As we are looking for only one subset, if any of the one among taken or not taken returns true, we can return true from our function. Therefore, we return ‘or(||)’ of both of them.
The final pseudocode after steps 1, 2, and 3:
 Recursion Base Conditions
If target == 0, it means that we have already found the subsequence from the previous steps, so we can return true.
If ind==0, it means we are at the first element, so we need to return arr[ind]==target. If the element is equal to the target we return true else false.
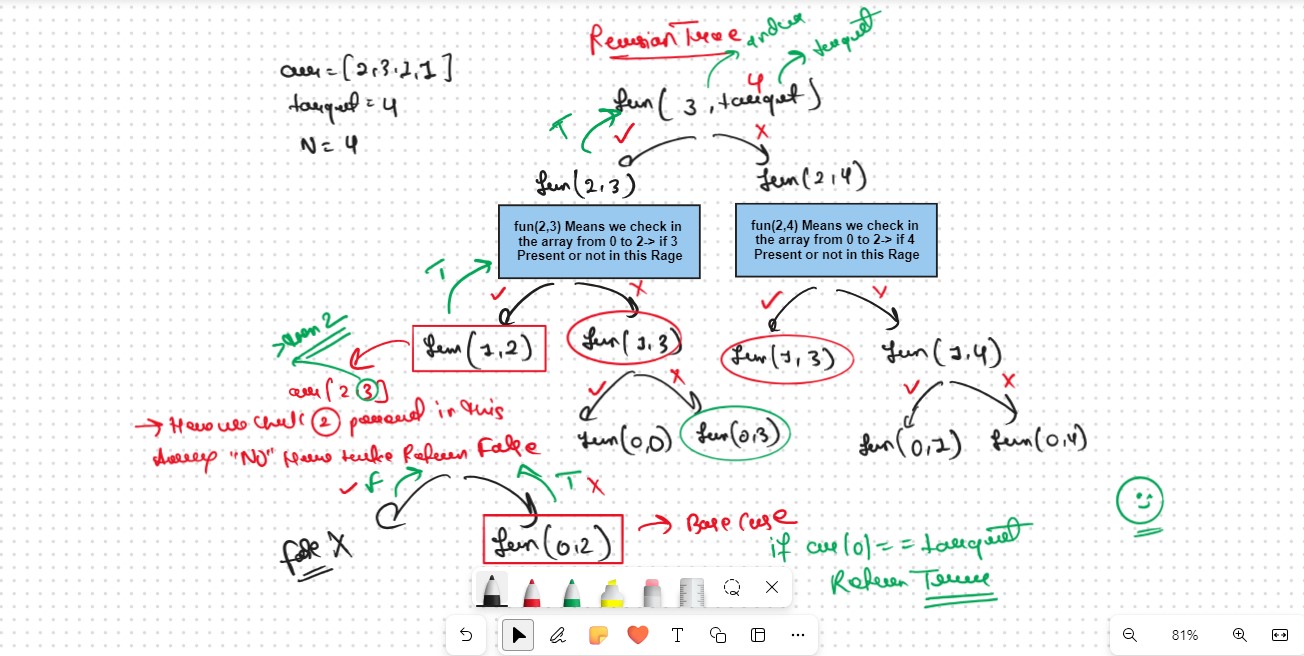
Recursion Tree
Recursion Base Conditions
If target == 0, it means that we have already found the subsequence from the previous steps, so we can return true.
If ind==0, it means we are at the first element, so we need to return arr[ind]==target. If the element is equal to the target we return true else false.
Recursion Tree
Recursion Java Code
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity: O(2^N)
Reason: Exponential Time we find out the all the Possible Path
Space Complexity: O(N)
Reason: We are using a recursion stack space(O(N))
Memoization Approch
If we observe in the recursion tree, we will observe a many number of overlapping subproblems. Therefore the recursive solution can be memoized for to reduce the time complexity.
 Steps to convert Recursive code to memoization solution:
Create a dp array of size [n][k+1]. The size of the input array is ‘n’, so the index will always lie between ‘0’ and ‘n-1’. The target can take any value between ‘0’ and ‘k’. Therefore we take the dp array as dp[n][k+1]
We initialize the dp array to -1.
Whenever we want to find the answer of particular parameters (say f(ind,target)), we first check whether the answer is already calculated using the dp array(i.e dp[ind][target]!= -1 ). If yes, simply return the value from the dp array.
If not, then we are finding the answer for the given value for the first time, we will use the recursive relation as usual but before returning from the function, we will set dp[ind][target] to the solution we get.
Steps to convert Recursive code to memoization solution:
Create a dp array of size [n][k+1]. The size of the input array is ‘n’, so the index will always lie between ‘0’ and ‘n-1’. The target can take any value between ‘0’ and ‘k’. Therefore we take the dp array as dp[n][k+1]
We initialize the dp array to -1.
Whenever we want to find the answer of particular parameters (say f(ind,target)), we first check whether the answer is already calculated using the dp array(i.e dp[ind][target]!= -1 ). If yes, simply return the value from the dp array.
If not, then we are finding the answer for the given value for the first time, we will use the recursive relation as usual but before returning from the function, we will set dp[ind][target] to the solution we get.
Memoization Java Code
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity:O(N*K) + O(N)
Reason: There are N*K states therefore at max ‘N*K’ new problems will be solved and we are running a for loop for ‘N’ times to calculate the total sum.
Space Complexity: O(N*K) + O(N)
Reason: We are using a recursion stack space(O(N)) and a 2D array ( O(N*K)).
Tabulation Approch
Tabulation is a
‘bottom-up’ approach where we start from the base case and reach the final answer that we want and Memoization is the
Top-down Approch.
In Tabulation Approch We Just Creat a DP Array Same as Memoization and Simply Convert the Recurance Relation into the form of the Looping
Steps to convert Recursive Solution to Tabulation one.
To convert the memoization approach to a tabulation one, create a dp array with the same size as done in memoization. We can set its type as bool and initialize it as false.
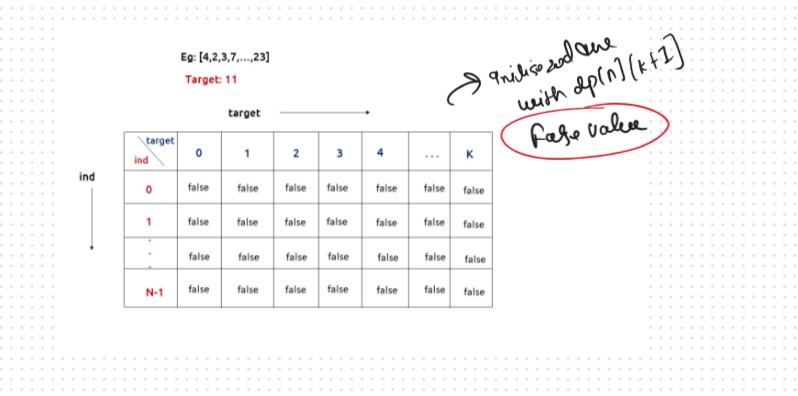 First, we need to initialize the base conditions of the recursive solution.
First, we need to initialize the base conditions of the recursive solution.
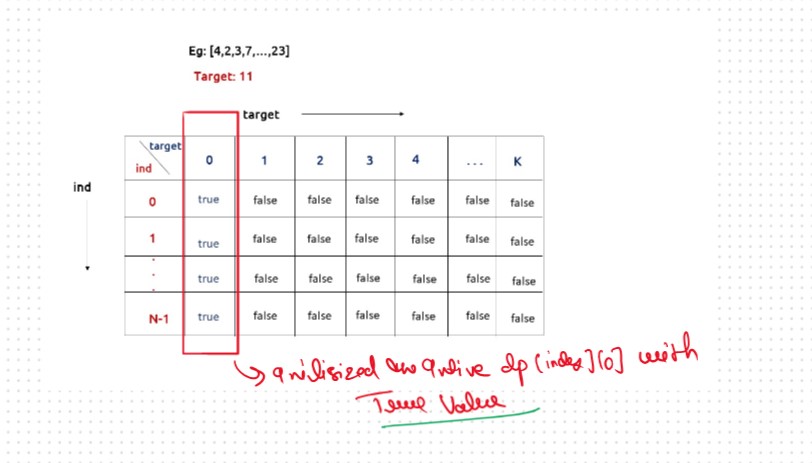 If target == 0, ind can take any value from 0 to n-1, therefore we need to set the value of the first column as true.
If target == 0, ind can take any value from 0 to n-1, therefore we need to set the value of the first column as true.
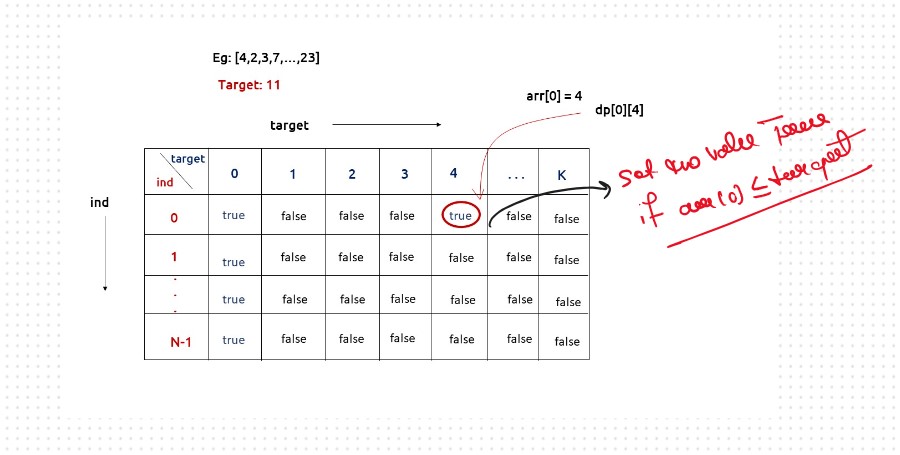 The first row dp[0][] indicates that only the first element of the array is considered, therefore for the target value equal to arr[0], only cell with that target will be true, so explicitly set dp[0][arr[0]] =true, (dp[0][arr[0]] means that we are considering the first element of the array with the target equal to the first element itself). Please note that it can happen that arr[0]>target, so we first check it: if(arr[0]<=target) then set dp[0][arr[0]] = true.
After that , we will set our nested for loops to traverse the dp array and following the logic discussed in the recursive approach, we will set the value of each cell. Instead of recursive calls, we will use the dp array itself.
At last we will return dp[n-1][k] as our answer.
The first row dp[0][] indicates that only the first element of the array is considered, therefore for the target value equal to arr[0], only cell with that target will be true, so explicitly set dp[0][arr[0]] =true, (dp[0][arr[0]] means that we are considering the first element of the array with the target equal to the first element itself). Please note that it can happen that arr[0]>target, so we first check it: if(arr[0]<=target) then set dp[0][arr[0]] = true.
After that , we will set our nested for loops to traverse the dp array and following the logic discussed in the recursive approach, we will set the value of each cell. Instead of recursive calls, we will use the dp array itself.
At last we will return dp[n-1][k] as our answer.
Tabulation Java Code
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity: O(N*K) +O(N)
Reason:There are two nested loops that account for O(N*K) and at starting we are running a for loop to calculate totSum.
Space Complexity: O(N*K)
Reason: We are using an external array of size ‘N*K’’.
Space Optimization
If we closelly Observed if any Tabulation Approch we used the Some Limited Stuff like: dp[ind][target] = dp[ind-1][target] || dp[ind-1][target-arr[ind]] for the finding the our ans then definetly here Spaced Optimization is Possible in that types of Problems. Always Remember
Golden Rule
If we required only Prev row and Prev Collom then definetly we can Space Optimized
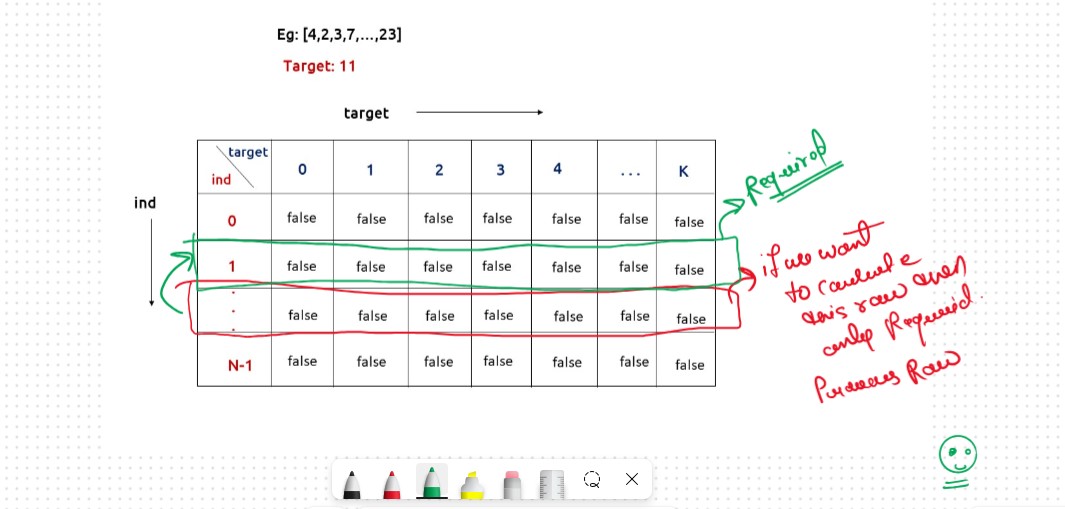
We see that we only need the previous row and column, in order to calculate curr[i]. Therefore we can space optimize it.
Initially, we can take a dummy row ( say prev) and initialize it as False.
Now the current row(say temp) only needs the previous row value and the current row’s value in order to curr[i].
Whenever we create a new row ( say cur), we need to explicitly set its first element is true according to our base condition.
At last prev[k] will give us the required answer.
SpaceOptmized Python Code
SpaceOptmized Java Code
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity: O(N*K) +O(N)
Reason: There are two nested loops that account for O(N*K) and at starting we are running a for loop to calculate totSum.
Space Complexity: O(K)
Reason: We are using an external array of size ‘K+1’ to store only one row.
Interview Docs File "All the Best" Team @DSAwithPrinceSingh


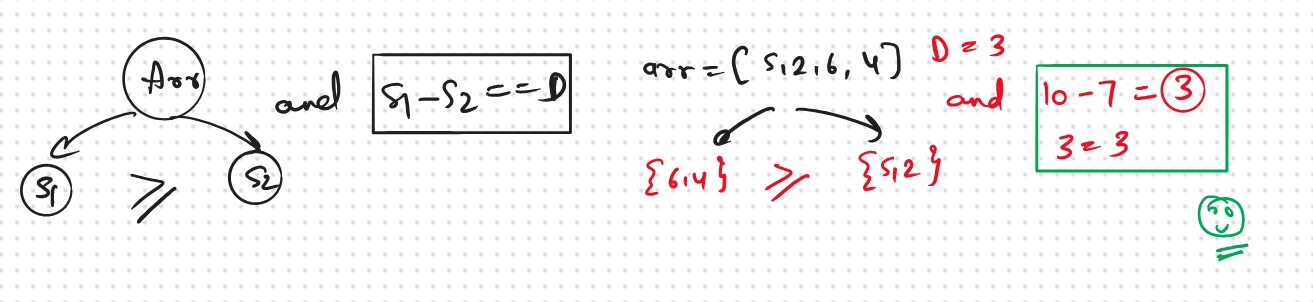






.png)
.png)

.png)
.png)



.png)
.png)

.png)
.png)