JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

DPL2 Climbing Staris

You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:
Input:n = 2
Output: 2
Explanation:
There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:
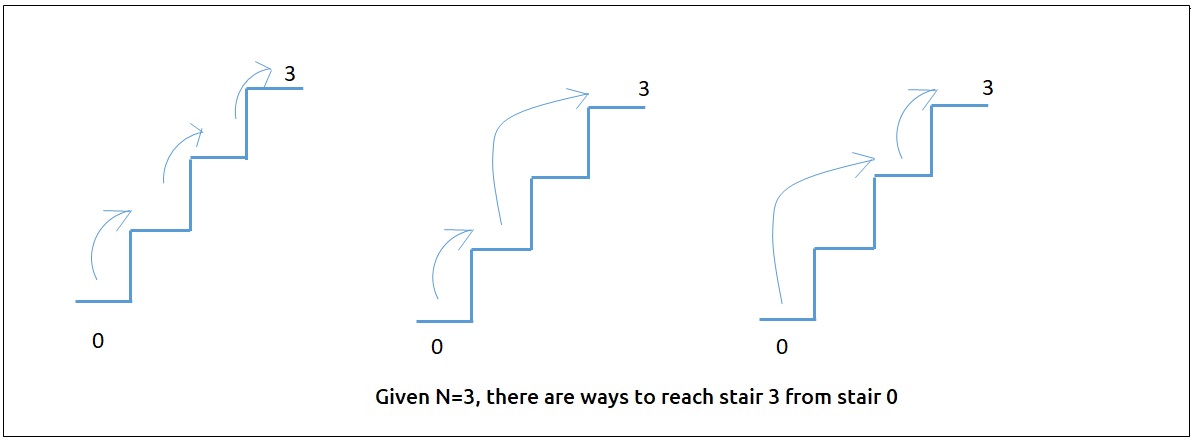
Input: n = 3
Output: 3
Explanation:
There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Constraints:
- 1 <= n <= 45

This Problem is Based on the Prevesouly that Problem that we learned in DPL1. Now there is the Question and that question is:-

Important Point

How to Identify a DP problem?
When we see a problem, it is very important to identify it as a dynamic programming problem. Generally (but not limited to) if the problem statement asks for the following:

Count the total number of ways

Given multiple ways of doing a task, which way will give the minimum or the maximum output

We can try to apply recursion. Once we get the recursive solution, we can go ahead to convert it to a dynamic programming one.

Steps To Solve The Problem After Identification
Once the problem has been identified, the following three steps comes handy in solving the problem:

Try to represent the problem in terms of indexes.

Try all possible choices/ways at every index according to the problem statement.

If the question states:-

Count all the ways – return sum of all choices/ways.

Find maximum/minimum- return the choice/way with maximum/minimum output.

Now uesing thes Concept we Solved the all upcoming DP Problems and Also this One.

Thought Process

We will assume n stairs as indexes from 0 to N.

At a single time, we have 2 choices: Jump one step or jump two steps. We will try both of these options at every index.

As the problem statement asks to count the total number of distinct ways, we will return the sum of all the choices in our recursive function.

he base case will be when we want to go to the 0th stair, then we have only one option.

There will be one more edge-case when n=1, if we call f(n-2) we will reach stair numbered -1 which is not defined, therefore we add an extra test case to return 1 ( the only way) when n=1.

Recurance Code

function(index) {
    if( index == 0) return 1
    if( index == 1) return 1
    return function(index-1) + function(index-2)
    }
                    

Time & Space Complexity

Time Complexity: O(2 ^ N)
Reason: Exponential Time we find out the all the Possible Path
Space Complexity: O(N)
Reason: We are using a recursion stack space(O(N))

Memoization Approch

Steps to memoize a recursive solution:
Any recursive solution to a problem can be memoized using these three steps:

Create a dp[n+1] array initialized to -1.

Whenever we want to find the answer of a particular value (say n), we first check whether the answer is already calculated using the dp array(i.e dp[n]!= -1 ). If yes, simply return the value from the dp array.

If not, then we are finding the answer for the given value for the first time, we will use the recursive relation as usual but before returning from the function, we will set dp[n] to the solution we get.

Time & Space Complexity

Time Complexity: O(N)
Reason: The overlapping subproblems will return the answer in constant time O(1). Therefore the total number of new subproblems we solve is ‘n’. Hence total time complexity is O(N).
Space Complexity: O(N)
Reason: We are using a recursion stack space(O(N)) and an array (again O(N)). Therefore total space complexity will be O(N) + O(N) ≈ O(N)

Tabulation Approch

Tabulation is a ‘bottom-up’ approach where we start from the base case and reach the final answer that we want.

Steps to convert Recursive Solution to Tabulation one.

Declare a dp[] array of size n+1.

First initialize the base condition values, i.e i=0 and i=1 of the dp array as 0 and 1 respectively.

Set an iterative loop that traverses the array( from index 2 to n) and for every index set its value as dp[i-1] + dp[i-2].

Time & Space Complexity

Time Complexity: O(N)
Reason: We are running a simple iterative loop
Space Complexity: O(N)
Reason: We are using an external array of size ‘n+1’.

Space Optimization

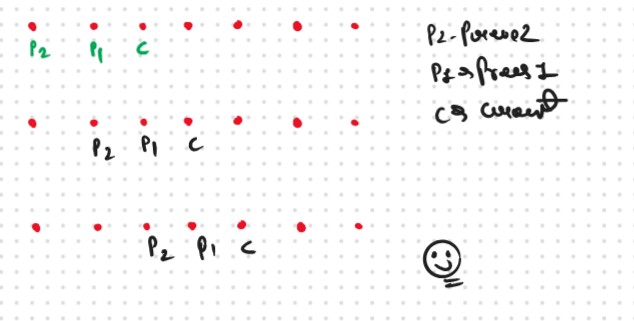
If we closely look at the relation,
dp[i] = dp[i-1] + dp[i-2] we see that for any i, we do need only the last two values in the array. So is there a need to maintain a whole array for it?
The answer is ‘No’. Let us call dp[i-1] as prev and dp[i-2] as prev2. Now understand the following illustration.

Each iteration’s cur_i and prev becomes the next iteration’s prev and prev2 respectively.

Therefore after calculating cur_i, if we update prev and prev2 according to the next step, we will always get the answer.

After the iterative loop has ended we can simply return prev as our answer.

Time & Space Complexity

Time Complexity: O(N)
Reason: We are running a simple iterative loop
Space Complexity: O(1)
Reason: We are not using any extra space Only Used a 2 Variables fro Storing the Prev Result.