JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

DPL20 Minimum Coins I "Infinite Supplies Pattern"

We are given a target sum of ‘X’ and ‘N’ distinct numbers denoting the coin denominations. We need to tell the minimum number of coins required to reach the target sum. We can pick a coin denomination for any number of times we want.

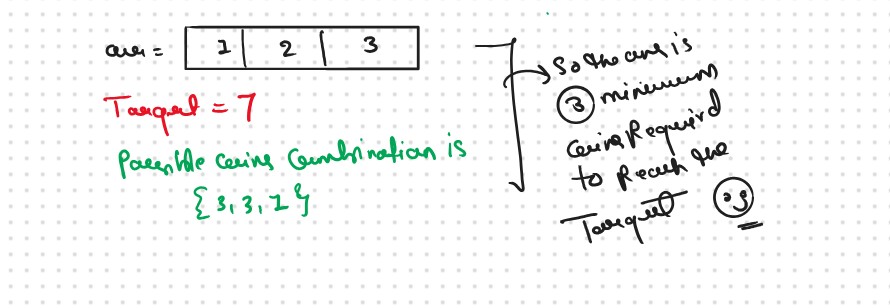Why a Greedy Solution doesn’t work?

The first approach that comes to our mind is greedy. A greedy solution will fail in this problem because there is no ‘Uniformity’ in data. While selecting a local better choice we may choose an item that will in long term give less value.

Let us understand this with help of an example

Gready Work on the Principle on Best Option on the Every Position

According to the Gready we Want the {9,1,1}. Coins to reach the Taget = 11 Ans: 3

But According to the Non-Gready Approch We Want {6,5}. Coins to reach the Taget = 11 Ans: 2

As the greedy approach doesn’t work, we will try to generate all possible combinations using recursion and select the combination which gives us the minimum number of coins.

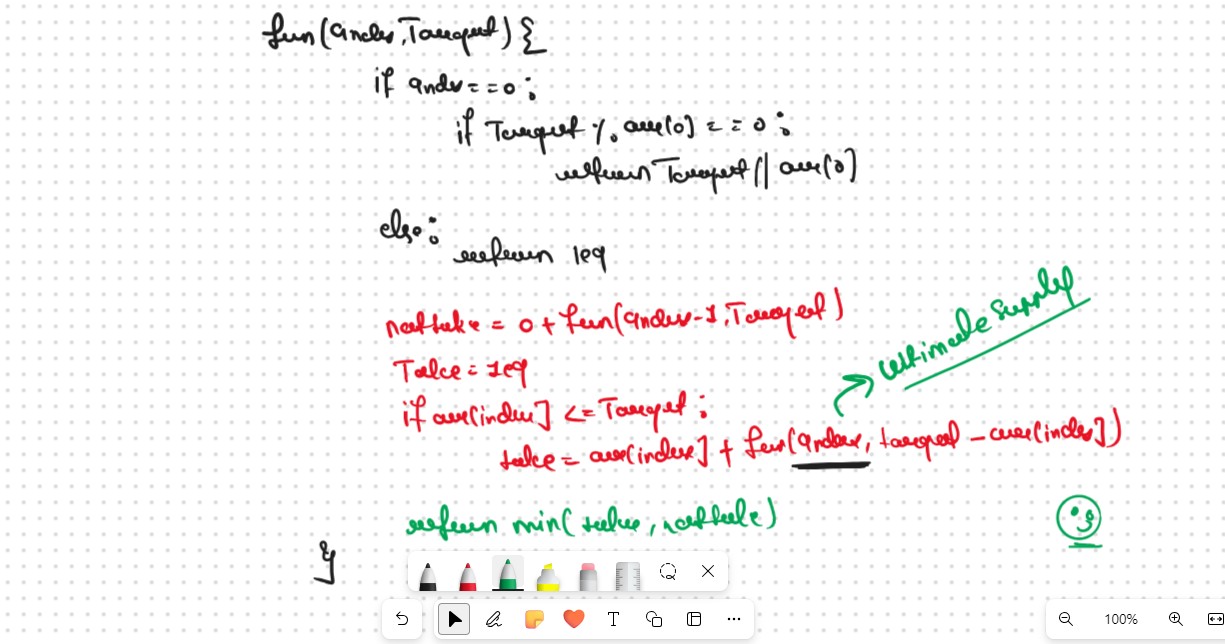
Recursice Approch

Steps to form the Recursive Solution
Step 1: Express the problem in terms of indexes.

We are given ‘n’ distinct numbers. Their denomination is represented by the ‘arr’ array. So clearly one parameter will be ‘ind’, i.e index up to which the array items are being considered.
There is one more parameter “Target”. We need to know the given target that we want to achieve
So, we can say that initially, we need to find fun(n-1, Target) where T is the initial target given to us. fun(n-1, Target) means we are finding the minimum number of coins required to form the target sum by considering coins from index 0 to n-1.

Our Base Case

If ind==0, it means we are at the first item, so in that case, the following cases can arise.

arr[0] = 4 and T = 12In such a case where the target is divisible by the coin element (T%arr[0]==0), we will return T // arr[0]

arr[0] =4 and T=1 , arr[0]=3 T=10In all other cases, we will not be able to form a solution (T%arr[0]!=0), so we will return a big number like 1e9

Step 2: Try out all possible choices at a given index.

We need to generate all the subsequences. We will use the pick/non-pick technique as discussed in, That we All Ready Learn in the Recursion Series.

We have two choices:

Exclude the current element in the subsequence: We first try to find a subsequence without considering the current index coin. If we exclude the current coin, the target sum will not be affected and the number of coins added to the solution will be 0. So we will call the recursive function fun(ind-1,Target)

Include the current element in the subsequence: We will try to find a subsequence by considering the current ith coin. As we have included the coin, the target sum will be updated to T-arr[ind] and we have considered 1 coin to our solution.

VVVV Important Point

Now here is the catch, as there is an unlimited supply of coins, we want to again form a solution with the same coin value. So we will not recursively call for f(ind-1, T-arr[ind]) rather we will stay at that index only and call for f(ind, T-arr[ind]) to find the answer.

Note: We will consider the current coin only when its denomination value (arr[ind]) is less than or equal to the target.

Step 3: Return the maximum of take and notTake

As we have to return the minimum number of coins, we will return the minimum of take and notTake as our answer.

The final pseudocode after steps 1, 2, and 3:

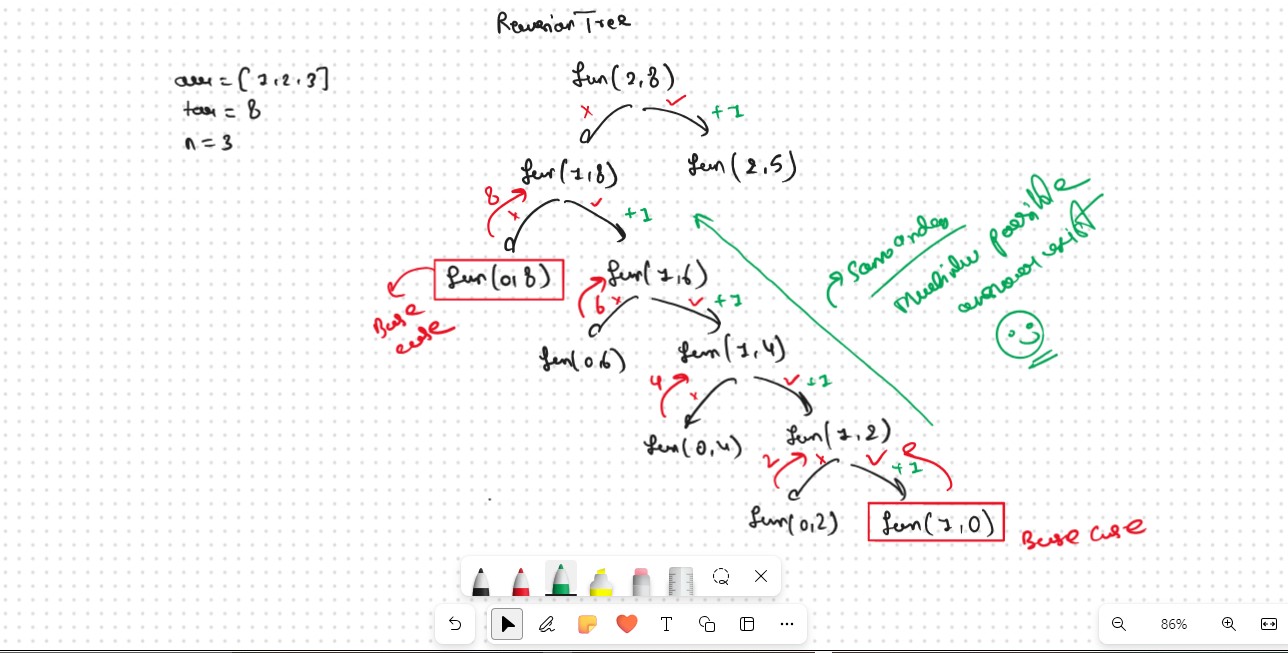
Recursion Tree

Time & Space Complexity

Time Complexity: O(2^N)
Reason: Exponential Time we find out the all the Possible Path
Space Complexity: O(N)
Reason: We are using a recursion stack space(O(N))

Memoization Approch

If we observe in the recursion tree, we will observe a many number of overlapping subproblems. Therefore the recursive solution can be memoized for to reduce the time complexity.

Steps to convert Recursive code to memoization solution:

CCreate a dp array of size [n][T+1]. The size of the input array is ‘N’, so the index will always lie between ‘0’ and ‘n-1’. The target Sum can take any value between ‘0’ and ‘T’. Therefore we take the dp array as dp[n][T+1]

We initialize the dp array to -1.

Whenever we want to find the answer of particular parameters (say f(ind,T)), we first check whether the answer is already calculated using the dp array(i.e dp[ind][T]!= -1 ). If yes, simply return the value from the dp array.

If not, then we are finding the answer for the given value for the first time, we will use the recursive relation as usual but before returning from the function, we will set dp[ind][target] to the solution we get.

Time & Space Complexity

Time Complexity:O(N*T)
Reason: There are N*T states therefore at max ‘N*T’ new problems will be solved.
Space Complexity: O(N*T) + O(N)
Reason: We are using a recursion stack space(O(N)) and a 2D array ( O(N*T)).

Tabulation Approch

Tabulation is a ‘bottom-up’ approach where we start from the base case and reach the final answer that we want and Memoization is the Top-down Approch.

In Tabulation Approch We Just Creat a DP Array Same as Memoization and Simply Convert the Recurance Relation into the form of the Looping

Steps to convert Recursive Solution to Tabulation one.

To convert the memoization approach to a tabulation one, create a dp array with the same size as done in memoization. We can initialize it as 0.

First, we need to initialize the base conditions of the recursive solution.

At ind==0, we are considering the first element, if T%arr[0] ==0, we initialize it to T/arr[0] else we initialize it to 1e9.

Next, we are done for the first row, so our ‘ind’ variable will move from 1 to n-1, whereas our ‘target’ variable will move from 0 to ‘T’. We will set the nested loops to traverse the dp array.

Inside the nested loops we will apply the recursive logic to find the answer of each cell.

When the nested loop execution has ended, we will return dp[n-1][T] as our answer.

Time & Space Complexity

Time Complexity: O(N*T)
Reason:There are 2 nested loops
Space Complexity: O(N*T)
Reason: We are using an external array of size ‘N*T’. Stack Space is eliminated.

Space Optimization

If we closelly Observed if any Tabulation Approch we used the Some Limited Stuff like: dp[ind][target] = dp[ind-1][target] + dp[ind-1][target-arr[ind]] for the finding the our ans then definetly here Spaced Optimization is Possible in that types of Problems. Always Remember

Golden Rule

If we required only Prev row and Prev Collom then definetly we can Space Optimized

We see that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it.

Time & Space Complexity

Time Complexity: O(N*T)
Reason: There are three 2 nested loops
Space Complexity: O(T)
Reason: We are using two external arrays of size ‘T+1’.