JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)
DPL26 Print Longest Common Subsequence
In the previous Question DPL25 Longest Common Subsequence, we learned to print
the length of the longest common subsequence of two strings. In this Question, we
will learn to print the actual string of the longest common subsequence.
 In This Question We Implement the Concept of the Backtracking
Here We Can not used Recursion & Memoization & Space Optimization Approch Becouse We Required the previous Data
This Types of Question Based on Tabulation Approch
Remaining Concept and Logic Will Be Same As We Follow in the DPL25 Only here we print the LCS
Intuition & Algorithm
Let us consider the following example
In This Question We Implement the Concept of the Backtracking
Here We Can not used Recursion & Memoization & Space Optimization Approch Becouse We Required the previous Data
This Types of Question Based on Tabulation Approch
Remaining Concept and Logic Will Be Same As We Follow in the DPL25 Only here we print the LCS
Intuition & Algorithm
Let us consider the following example

In DP25 There in the tabulation approach, we declared a dp array and dp[n][m] will have the length of the longest common subsequence., i.e dp[n][m] = 3.
Now, with help of two nested loops, if we print the dp array, it will look like this
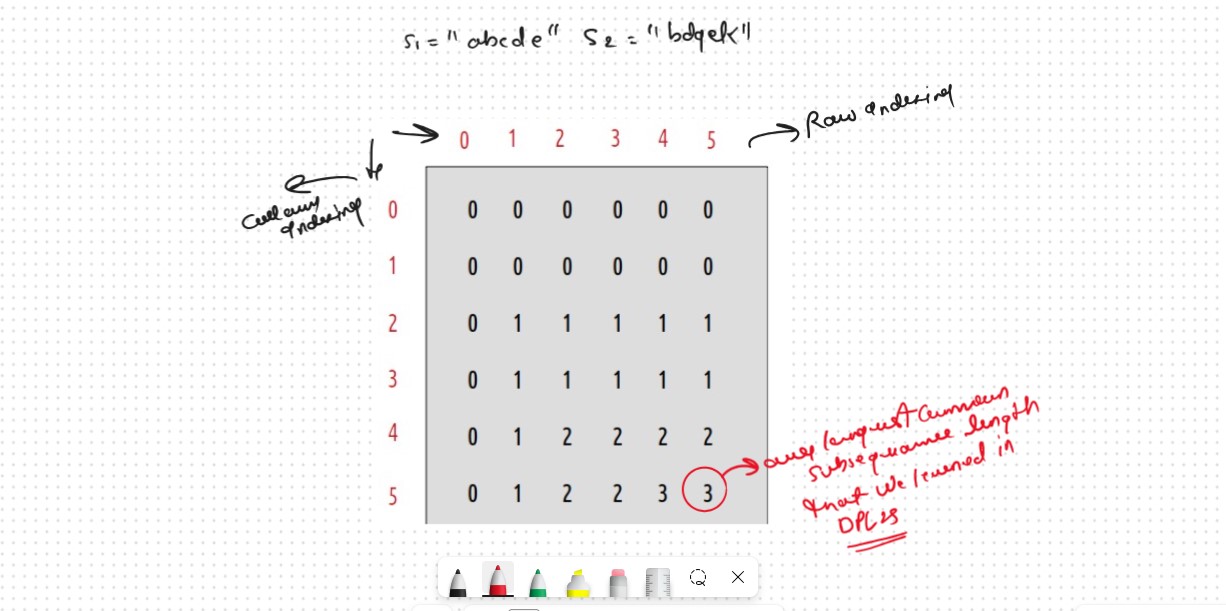
Here dp[5][5] gives us the length of the longest common subsequence: 3.
Now let us try to form the string itself. We know its length already. We give it the name StringArray.
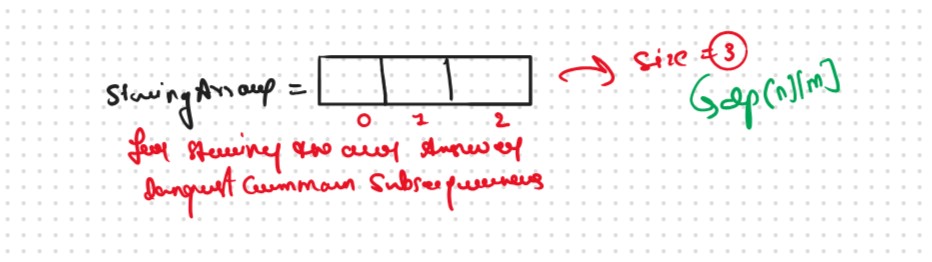 We will use the dp array to form the LCS string. For that, we need to think, about how did the dp array was originally filled. The tabulation approach used 1-based indexing. We also write the characters corresponding to the indexes of the dp array
We will use the dp array to form the LCS string. For that, we need to think, about how did the dp array was originally filled. The tabulation approach used 1-based indexing. We also write the characters corresponding to the indexes of the dp array
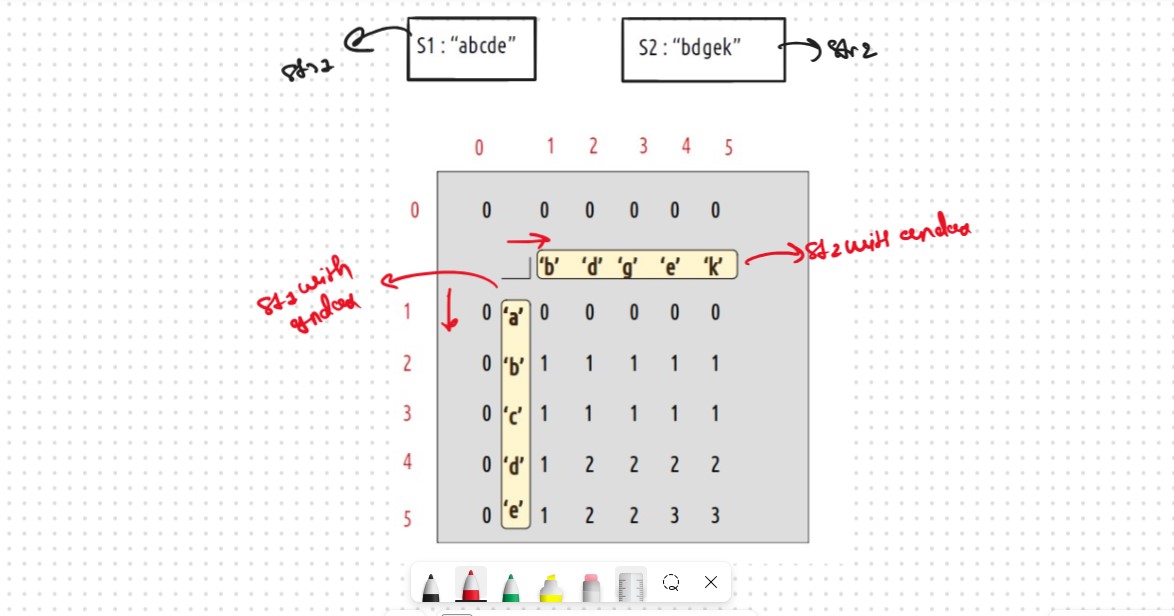
Now, let us see what were the 2 conditions that we used while forming the dp array and Store the Ans on the Basis of these Condition
if(S1[i-1] == S2[j-1]), then return 1 + dp[i-1][j-1]
if(S1[i-1] != S2[j-1]), then return 0 + max(dp[i-1][j],dp[i][j-1])
These two conditions along with the dp array give us all the required information required to print the LCS string.
Approach
The algorithm approach is stated below
We will fill the string str from the last by maintaining a pointer.
We will start from the right most cell of the dp array, initially i=n and j=m.
At every cell, we will check if S1[i-1] == S2[j-1], if it is then it means this character is a part of the longest common substring. So we will push it to the str (at last). Then we will move to the diagonally top-left(↖️) cell by assigning i to i-1 and j to j-1.
Else, this character is not a part of the longest common subsequence. It means that originally this cell got its value from its left cell (←) or from its top cell (↑). Whichever cell’s value will be more of the two, we will move to that cell.
We will continue till i>0 and j>0, failing it we will break from the loop.
At last we will get our lcs string in “str”.
Let's Dry Run and Understand the Concept Behind the Logic
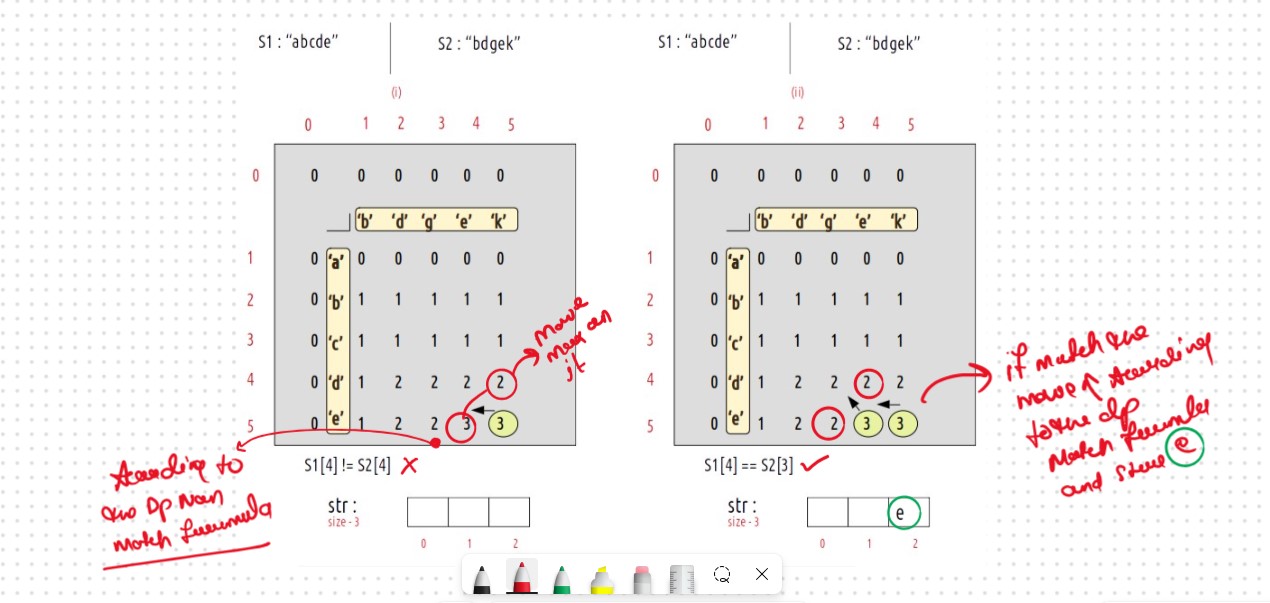 At starting i=5 and j=5
As S1[4] != S2[4], we move to the left side (←) as it’s value is greater than the top value(↑), therefore i=5 and j=4
As S1[4] == S2[3], we add the current character to the str string(at last) and move to i-1 and j-1 cell i.e top-left(↖️), therefore i=4 and j=3.
At starting i=5 and j=5
As S1[4] != S2[4], we move to the left side (←) as it’s value is greater than the top value(↑), therefore i=5 and j=4
As S1[4] == S2[3], we add the current character to the str string(at last) and move to i-1 and j-1 cell i.e top-left(↖️), therefore i=4 and j=3.
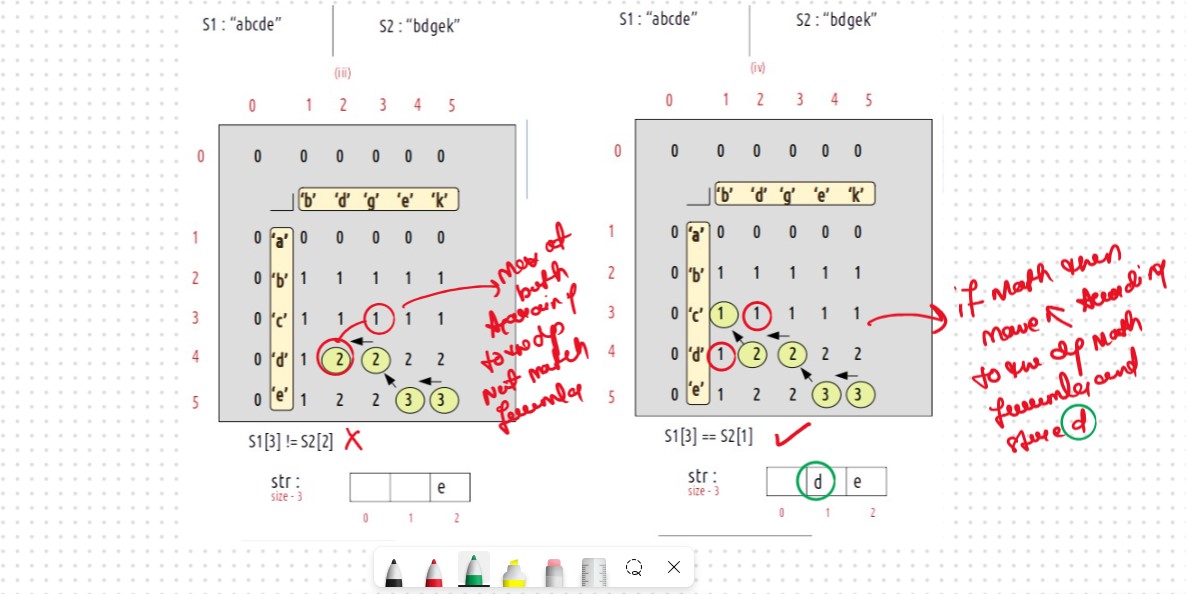 As S1[3] != S2[2], we move to the left cell (←) as its value is larger than the top cell(↑), i becomes 4 and j becomes 2.
As S1[3] == S2[1], we will add this character to str string and we will move to the top-left cell (↖️) i becomes 3 and j becomes 1
As S1[3] != S2[2], we move to the left cell (←) as its value is larger than the top cell(↑), i becomes 4 and j becomes 2.
As S1[3] == S2[1], we will add this character to str string and we will move to the top-left cell (↖️) i becomes 3 and j becomes 1
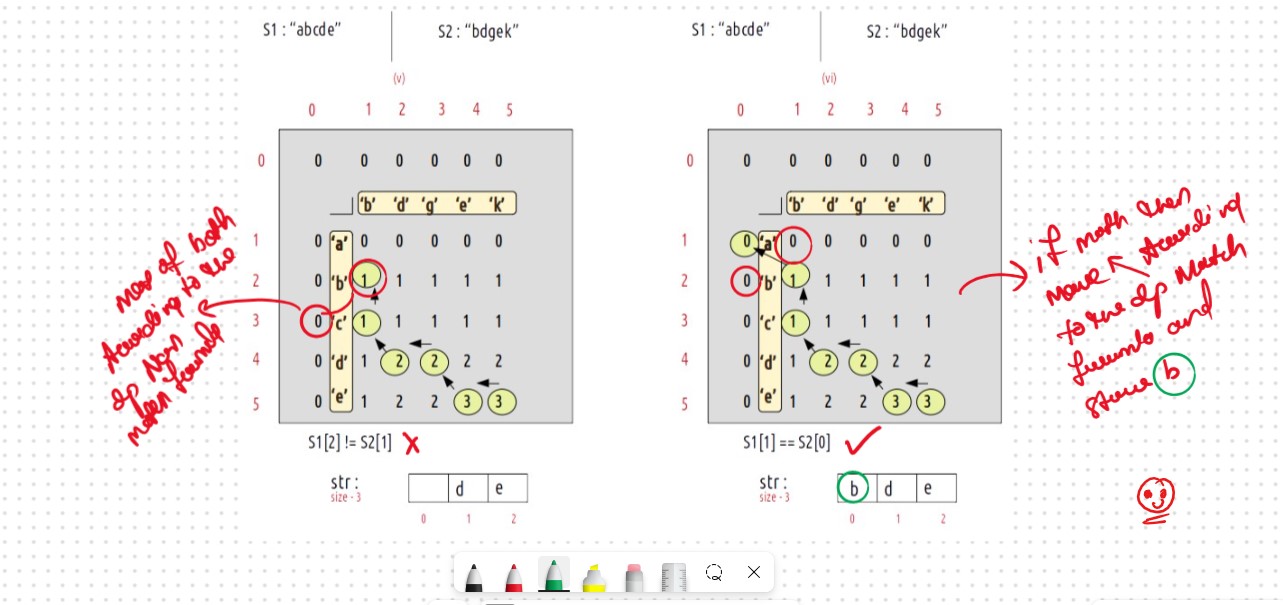 As S1[2] != S2[1], we will move to the top cell (↑) as its value is greater than the left cell (←). Now i become 2 and j remains 1.
As S1[1] == S2[0], we will add this character to str string and we will move to the top-left cell (↖️) i becomes 1 and j becomes 1 and j becomes 0.
As j is zero, we have hit the exit condition so we will break out of the loop and str contains the longest common subsequence.
As S1[2] != S2[1], we will move to the top cell (↑) as its value is greater than the left cell (←). Now i become 2 and j remains 1.
As S1[1] == S2[0], we will add this character to str string and we will move to the top-left cell (↖️) i becomes 1 and j becomes 1 and j becomes 0.
As j is zero, we have hit the exit condition so we will break out of the loop and str contains the longest common subsequence.
Tabulation Approch
Similer As DPL25
Tabulation is a
‘bottom-up’ approach where we start from the base case and reach
the final answer that we want and Memoization is the
Top-down Approch.
In Tabulation Approch We Just Creat a DP Array Same as Memoization and Simply
Convert the Recurance Relation into the form of the Looping
Steps to convert Recursive Solution to Tabulation one.
To convert the memoization approach to a tabulation one, create a dp array with the
same size as done in memoization. We can initialize it as 0.
Initialization: Shifting of indexes
In the recursive logic, we set the base case to if(ind1 < 0 || ind2 < 0) but we
can’t set the dp array’s index to -1. Therefore a hack for this issue is to
shift every index by 1 towards the right.
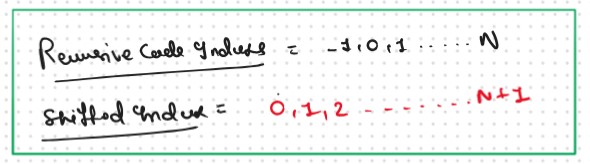 Therefore, now the base case will be if(ind1==0 || ind2==0).
Similarly, we will implement the recursive code by keeping in mind the shifting of
indexes, therefore S1[ind1] will be converted to S1[ind1-1]. Same for others.
At last we will print dp[N][M] as our answer.
Therefore, now the base case will be if(ind1==0 || ind2==0).
Similarly, we will implement the recursive code by keeping in mind the shifting of
indexes, therefore S1[ind1] will be converted to S1[ind1-1]. Same for others.
At last we will print dp[N][M] as our answer.
Tabulation Java Code
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity: O(N*M)
Reason:There are 2 nested loops
Space Complexity: O(N*M)
Reason: We are using an external array of size ‘(N*M)’. Stack Space is
eliminated.
Interview Docs File "All the Best" Team @DSAwithPrinceSingh
~ It's All About Consistency📈 Dedication🎯 HardWork💪 Happy Coding❤️ ~








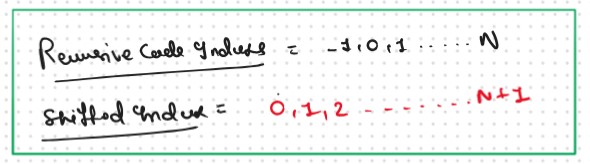
.png)
.png)