JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

DPL27 Longest Common Substring 🔥

Longest Common Substring A substring of a string is a subsequence in which all the characters are consecutive. Given two strings, we need to find the longest common substring.
We need to print the length of the longest common substring.

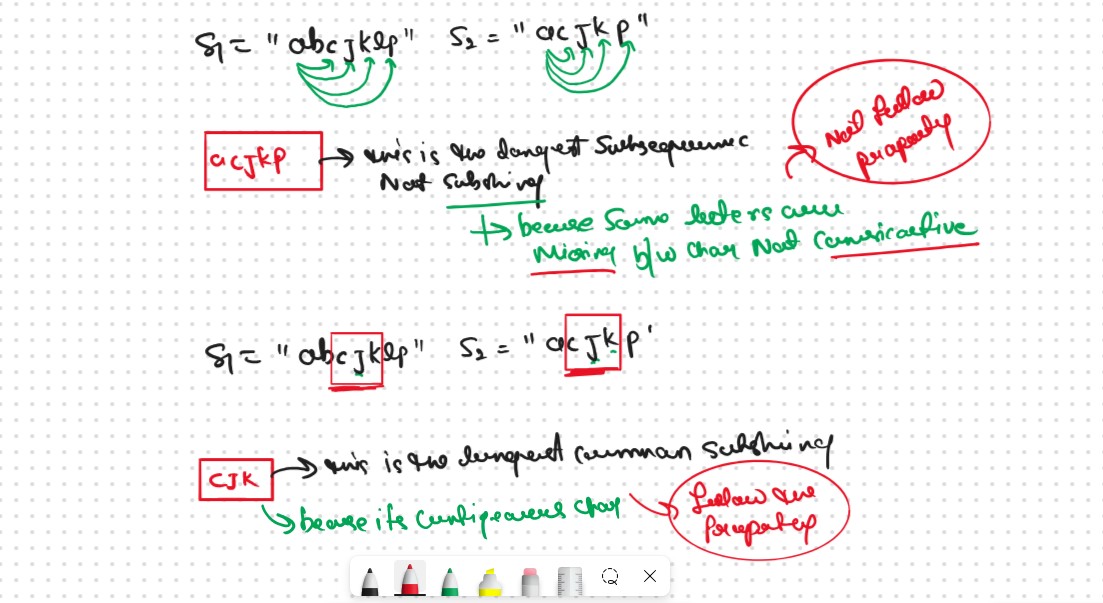
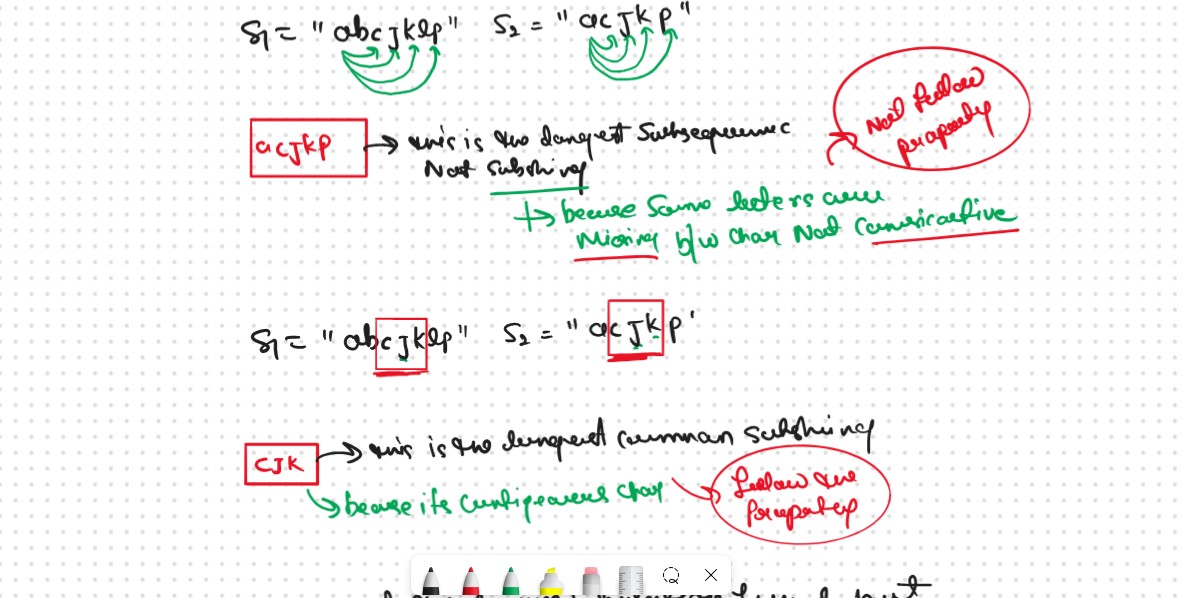
Again this Problem is the Modified Version of the DPL25 and DPL26

In Preveous 2 String on DP Problem we Solved the Problem Based on the Longest Common Subsequence

Burt this Problem based on the Longest Common Substring

Subsequence is Means its Maintain the Order and can not be Consecutive or Consecutive

Substring it has to be Consecutive

We Solved this Problem using the Tabulation Approch that we follow in the last 2 Problems that is DPL25 & DPL26 but here is Required the Certain Modification in the Tabulation Formula

According to the Longest Common Subsequence Tabulation Formula is

Matching: dp[i][j] = 1 + dp[i-1][j-1]

Not Matching: max(dp[i-1][j],dp[i][j-1])

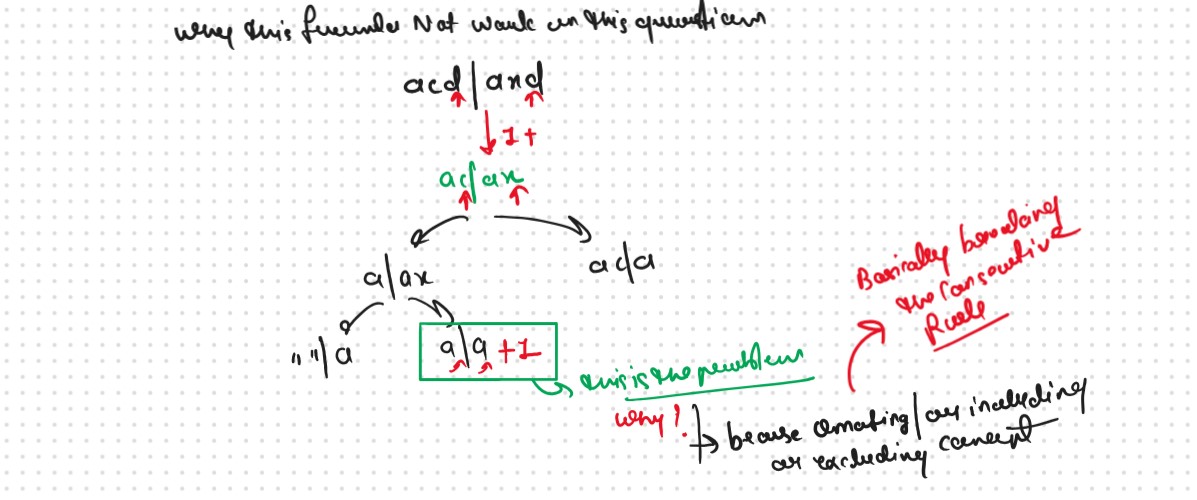
Why this Same Formula Not Work in this Problem

If We CareFully Observed then we See, So Problem is this: Not Matching: max(dp[i-1][j],dp[i][j-1]) Omating or Including or Excluding Concept when the str1[index1] != str2[index2] Becouse this Formual Break the Rule of the Consecutive String As we See in the Img.

Lets Understand How Tabulation work in this Probelm

In this Problem we used the a 3rd Variable So that's why we go eith the Tabulation Approch

We Also Go With Memoization and Recursion Approch if we Want Just Change the Not Matchng Formual and Everthing will be Same.

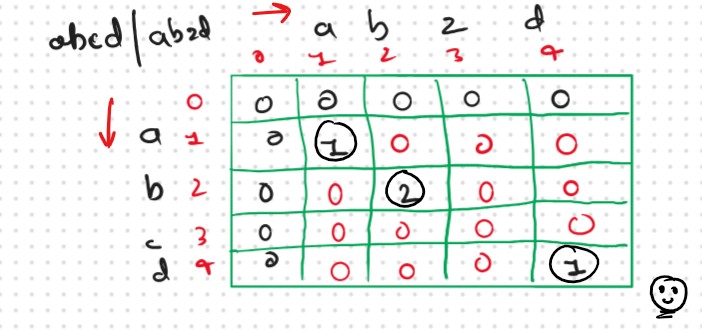
Some Important Point that we Observed During Crafting the Table

In Longest Common Subsequence We Depends on the Prev Row

In this Problem we are Not Depends on the Prev Row & Coll

if match str1[index1] == str2[index2] then Add the Prev row and coll cell Value According to the Match Formula

if Not Match then we Not Use max(dp[i-1][j],dp[i][j-1]) thsi Becouse its Break the Rule of the Consecutive String and We are Not Depends on the Prev row and coll So we Directly Put = 0 that is teh Modification in Palce of max(dp[i-1][j],dp[i][j-1])

dp[i][j] = 0 that is the Modification and Entire Process Will Be Same as Like in last 2 Problems that we Did It DPL25 & DPL26

Tabulation Approch

Tabulation is a ‘bottom-up’ approach where we start from the base case and reach the final answer that we want and Memoization is the Top-down Approch.

In Tabulation Approch We Just Creat a DP Array Same as Memoization and Simply Convert the Recurance Relation into the form of the Looping

Steps to convert Recursive Solution to Tabulation one.

To convert the memoization approach to a tabulation one, create a dp array with the same size as done in memoization. We can initialize it as 0.

if(S1[i-1] != S2[j-1]), the characters don’t match, therefore the consecutiveness of characters is broken. So we set the cell value (dp[i][j]) as 0.

if(S1[i-1] == S2[j-1]), then the characters match and we simply set its value to 1+dp[i-1][j-1]. We have done so because dp[i-1][j-1] gives us the longest common substring till the last cell character (current strings -{matching character}). As the current cell’s character is matching we are adding 1 to the consecutive chain.

Note: dp[n][m] will not give us the answer; rather the maximum value in the entire dp array will give us the length of the longest common substring. This is because there is no restriction that the longest common substring is present at the end of both the strings.

Time & Space Complexity

Time Complexity: O(N*M)
Reason:There are 2 nested loops
Space Complexity: O(N*M)
Reason: We are using an external array of size ‘N*M’. Stack Space is eliminated.

Space Optimization

If we closelly Observed if any Tabulation Approch we used the Some Limited Stuff like: dp[ind1-1][ ], dp[ind][ ] for the finding the our ans then definetly here Spaced Optimization is Possible in that types of Problems. Always Remember

Golden Rule

If we required only Prev row and Prev Collom then definetly we can Space Optimized

So we are not required to contain an entire array, we can simply have two rows prev and cur where prev corresponds to dp[ind-1] and cur to dp[ind].

After declaring prev and cur, replace dp[ind-1] to prev and dp[ind] with cur and after the inner loop executes, we will set prev = cur, so that the cur row can serve as prev for the next index.

Time & Space Complexity

Time Complexity: O(N*M)
Reason: There are three 2 nested loops
Space Complexity: O(M)
Reason: We are using an external array of size ‘M+1’ to store only two rows.