JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)
DPL31 Shortest Common Supersequence
We are given two strings ‘S1’ and ‘S2’. We need to return their shortest common supersequence. A supersequence is defined as the string which contains both the strings S1 and S2 as subsequences
What is the Meaning of the Shortest Common Supersequence?
It's Stae that you have a str1 and str2 and your task is making the Singhe Shortest String that contains the both String str1 and str2 that is the
defination of the Shortest Common Supersequence
Maintain the Order of the character not change the order of the character
Again thsi Question Based on the DPL25 and DPL26 with a Small Modification only need to Identify the Pattern
In This Question We Implement the Concept of the Backtracking
Here We Can not used Recursion & Memoization & Space Optimization Approch
Becouse We Required the previous Data
This Types of Question Based on Tabulation Approch
Intuition
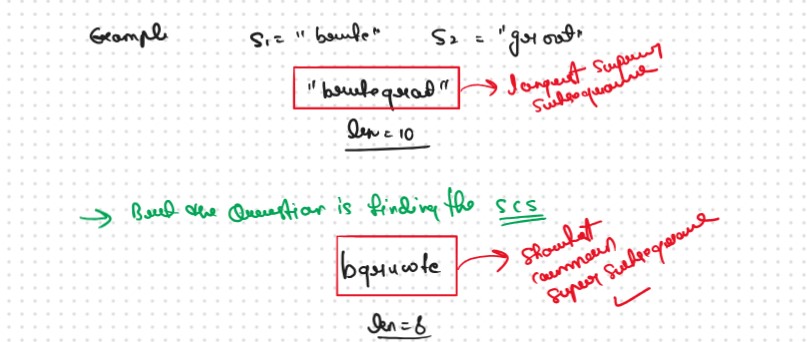
If i talk aboth the Brute force Approch then we Merged the Both String that is out Longest Common Supersequence
But in this Question we Required the Shortest Common Supersequence So what we can do?
If we think a little, there are some common characters that we can avoid writing for both the strings separately. These common characters can’t be all the common characters. They are the characters that are common and come in the same order. In other words, they are the characters of the longest common subsequence.
We keep tarck the longest common subsequence and put only once in the ans string
Maintaing the Order of the String and generate the ans string
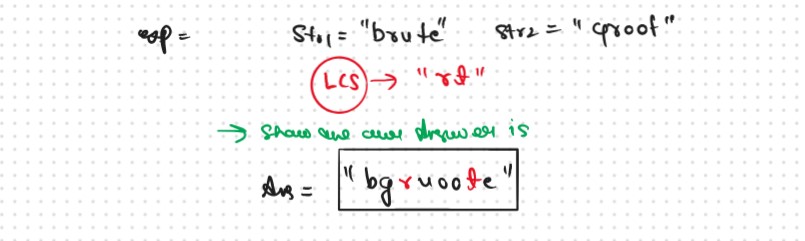
if we observer something then we used the Common char with Same Order once and then used the Remaining char of the both String, So this is Nothing but longest common subsequence So we can say that.
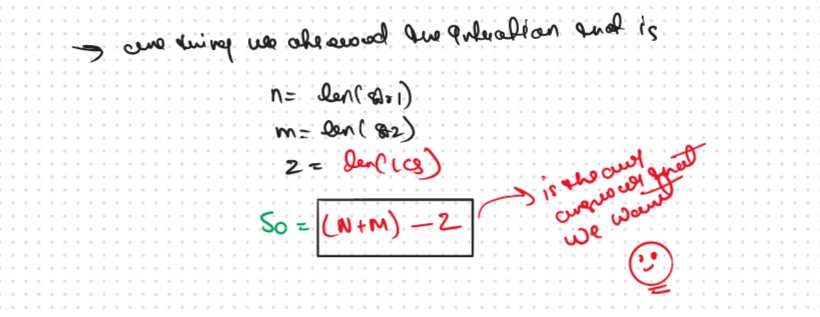
n = len(str1)
m = len(str2)
z = len(LCS)
So the our Shortest Common Supersequence answer is the nothing but (n+m) - z
Recursion Java Code
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Now Time to Print the Shortest Common Supersequence, Remaining Concept and Logic Will Be Same As We Follow in the DPL26 Only here we updaet the Some Condtion According to the Question let's See
When we form the DP table to calculate as we do in longest Common Subsequence (as well as in Print Longest Common Subsequence)
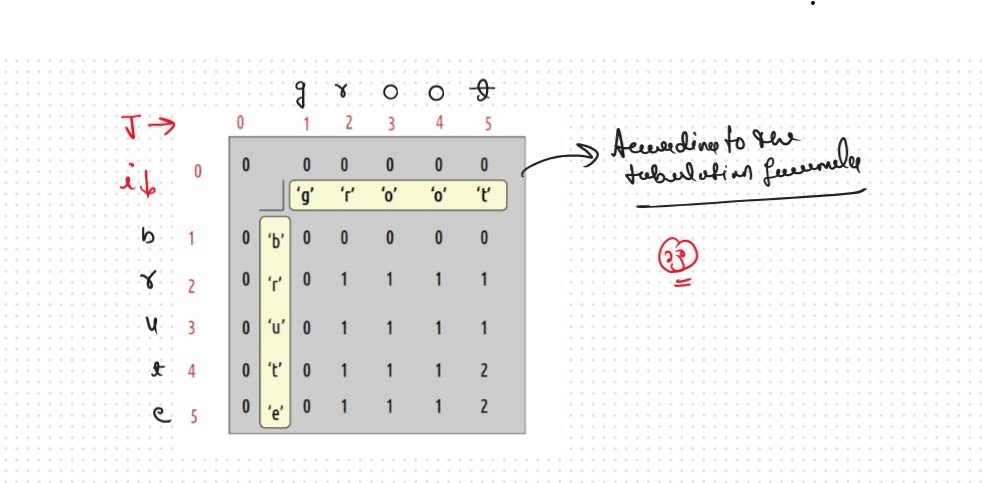
o frame the string, we need to understand how the dp table was formed and work in the reverse process.
Accroding to the Tabulation Condition we have 2 Case that is
if(S1[i-1] == S2[j-1]), then return 1 + dp[i-1][j-1]
if(S1[i-1] != S2[j-1]), then return 0 + max(dp[i-1][j],dp[i][j-1])
Approach
We will start from the right-most cell of the dp array, initially i=n and j=m
To form the string, we will work in a reverse manner.
f(S1[i-1] == S2[j-1]) this means the character is an lcs character and needs to be included only once from both the strings, so we add it to the ans string and reduce both i and j by 1 According to the if(S1[i-1] == S2[j-1]), then return 1 + dp[i-1][j-1]. We reduce them simultaneously to make sure the character is counted only once.
if(S1[i-1] != S2[j-1]) this means that the character is a non-lcscharacter and then we move the pointer to the top cell or left cell depending on which is greater According to the if(S1[i-1] != S2[j-1]), then return 0 + max(dp[i-1][j],dp[i][j-1]). This way non-lcs characters will be included separately in the right order.
How to Approch this Allogrithm and Implement
We start from cell dp[n][m]. Initially i=n and j=m.
At every cell, we will check if S1[i-1] == S2[j-1], if it is then it means this character is a part of the longest common subsequence. So we will push it to the ans string str. Then we will move to the diagonally top-left(↖️) cell by assigning i to i-1 and j to j-1.
Else, this character is not a part of the longest common subsequence so we include it in ans string. Originally this cell got its value from its left cell (←) or from its top cell (↑). Whichever cell’s value will be more of the two, we will move to that cell.
We will continue till i>0 and j>0, failing it we will break from the loop.
This is the Majore change in this Question that we not do in the DPL26 that is
After breaking, either i>0 or j>0 (only one condition will fail to break from the while loop), if(i>0) we push all the characters from S1 to ans string, else if(j>0), we push all the remaining characters from S2.
At last, we reverse the ‘ans’ string and we get our answer.
Let's Dry Run and Understand the Concept Behind the Logic
At starting i=5 and j=5
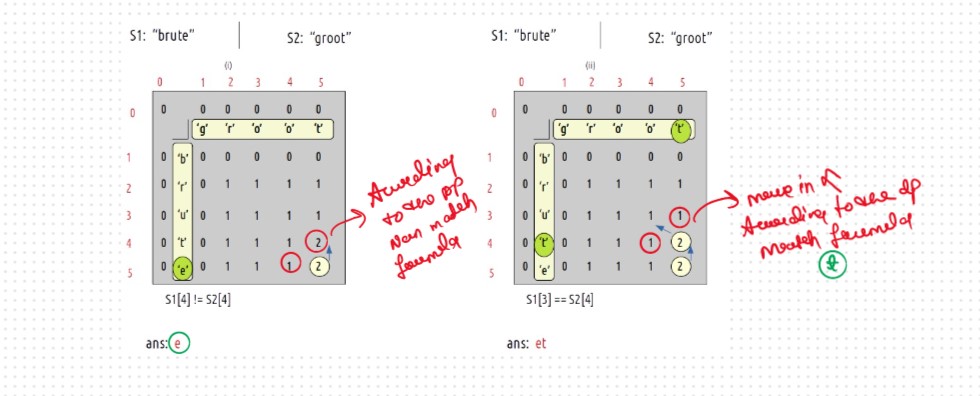 VVVVV Imp Point
As S1[4] != S2[4], we move to the top cell(↑) as its value is greater than the left cell(←) but before moving as we are leaving row 5(i=5) we just add S1[4] to our ans string. that is the Modification that we not do in the DPL26
As S1[3] == S2[4], this is an lcs-character. We add the current character to the ans string(and move to i-1 and j-1 cell) i.e top-left(↖️). Reducing i and j simultaneously helps in adding the lcs character only once in the ans string.
VVVVV Imp Point
As S1[4] != S2[4], we move to the top cell(↑) as its value is greater than the left cell(←) but before moving as we are leaving row 5(i=5) we just add S1[4] to our ans string. that is the Modification that we not do in the DPL26
As S1[3] == S2[4], this is an lcs-character. We add the current character to the ans string(and move to i-1 and j-1 cell) i.e top-left(↖️). Reducing i and j simultaneously helps in adding the lcs character only once in the ans string.
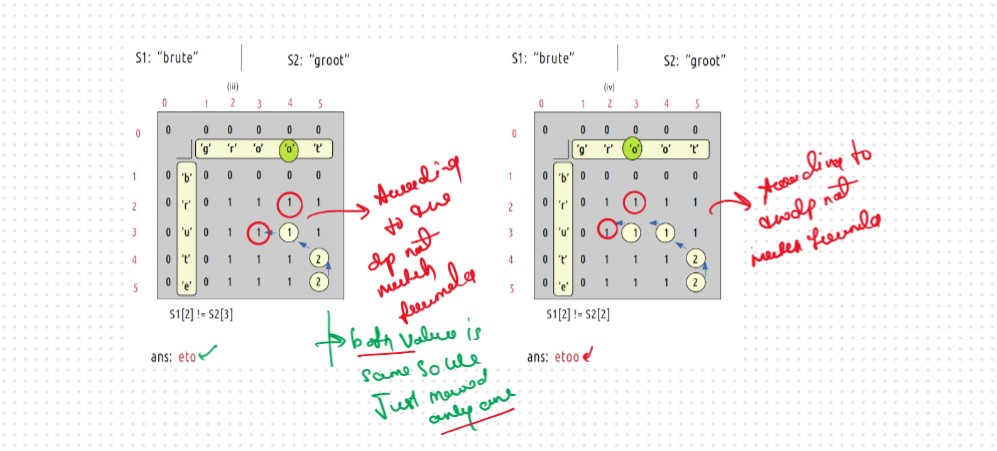 As S1[2] != S2[3], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 4 (j=4) and will not return to it so we add S2[3] to our ans string.
As S1[2] != S2[2], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 3 (j=3) and will not return to it so we add S2[2] to our ans string.
As S1[2] != S2[3], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 4 (j=4) and will not return to it so we add S2[3] to our ans string.
As S1[2] != S2[2], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 3 (j=3) and will not return to it so we add S2[2] to our ans string.
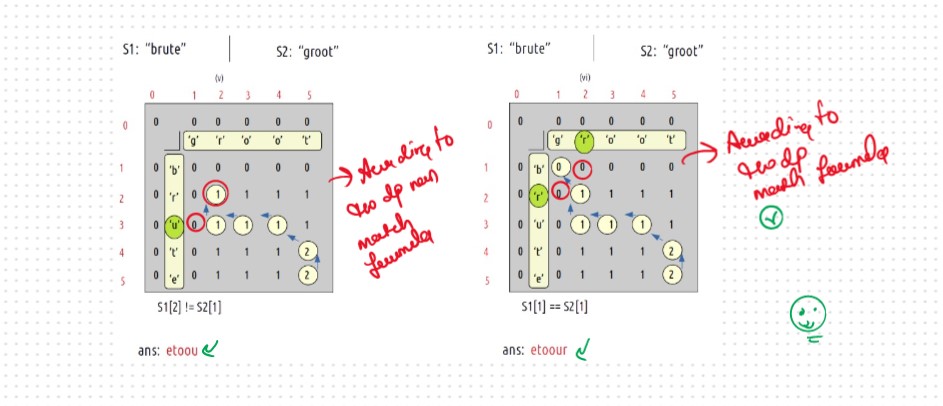 S1[2] != S2[1], we move to the top cell(↑) as its value is greater than the left cell(←) but before moving as we are leaving row 3(i=3) and will not return to it so we add S1[2] to our ans string.
As S1[1] == S2[1], this is an lcs-character. We add the current character to the ans string(and move to i-1 and j-1 cell) i.e top-left(↖️).
S1[2] != S2[1], we move to the top cell(↑) as its value is greater than the left cell(←) but before moving as we are leaving row 3(i=3) and will not return to it so we add S1[2] to our ans string.
As S1[1] == S2[1], this is an lcs-character. We add the current character to the ans string(and move to i-1 and j-1 cell) i.e top-left(↖️).
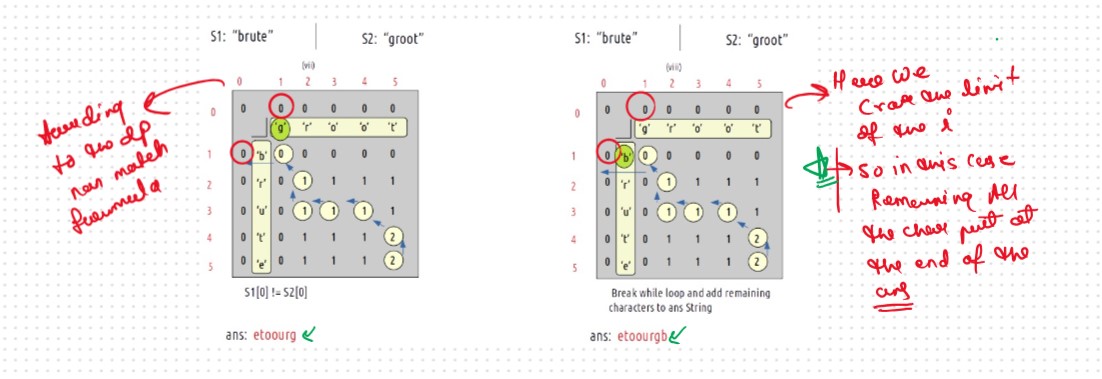 As S1[2] != S2[2], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 1 (j=1) and will not return to it so we add S2[0] to our ans string.
As j=0, we have reached the exit condition of the while loop, so we will break from it but still there are some characters left in the other string. We will simply add them in the ans string.
At last, we will return the reverse of the ans string as the final answer.
As S1[2] != S2[2], we move to the left cell(←) as its value is greater than or equal to the top cell(↑) but before moving as we are leaving column 1 (j=1) and will not return to it so we add S2[0] to our ans string.
As j=0, we have reached the exit condition of the while loop, so we will break from it but still there are some characters left in the other string. We will simply add them in the ans string.
At last, we will return the reverse of the ans string as the final answer.
Tabulation Approch
Similer As DPL25
Tabulation is a
‘bottom-up’ approach where we start from the base case and reach
the final answer that we want and Memoization is the
Top-down Approch.
In Tabulation Approch We Just Creat a DP Array Same as Memoization and Simply
Convert the Recurance Relation into the form of the Looping
Steps to convert Recursive Solution to Tabulation one.
To convert the memoization approach to a tabulation one, create a dp array with the
same size as done in memoization. We can initialize it as 0.
Initialization: Shifting of indexes
In the recursive logic, we set the base case to if(ind1 < 0 || ind2 < 0) but we
can’t set the dp array’s index to -1. Therefore a hack for this issue is to
shift every index by 1 towards the right.
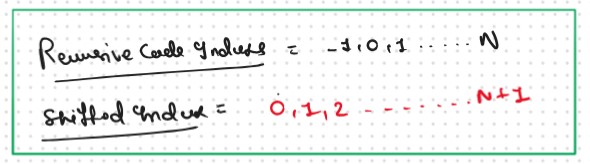 Therefore, now the base case will be if(ind1==0 || ind2==0).
Similarly, we will implement the recursive code by keeping in mind the shifting of
indexes, therefore S1[ind1] will be converted to S1[ind1-1]. Same for others.
At last we will print dp[N][M] as our answer.
Therefore, now the base case will be if(ind1==0 || ind2==0).
Similarly, we will implement the recursive code by keeping in mind the shifting of
indexes, therefore S1[ind1] will be converted to S1[ind1-1]. Same for others.
At last we will print dp[N][M] as our answer.
Tabulation Java Code
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity: O(N*M)
Reason:There are 2 nested loops
Space Complexity: O(N*M)
Reason: We are using an external array of size ‘(N*M)’. Stack Space is
eliminated.
Interview Docs File "All the Best" Team @DSAwithPrinceSingh
~ It's All About Consistency📈 Dedication🎯 HardWork💪 Happy Coding❤️ ~



.png)
.png)





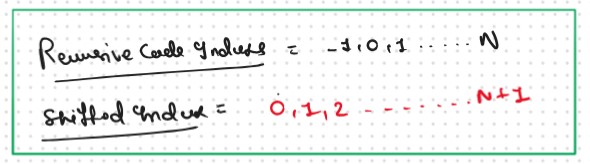
.png)
.png)