JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

DPL6 House Robber II

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.

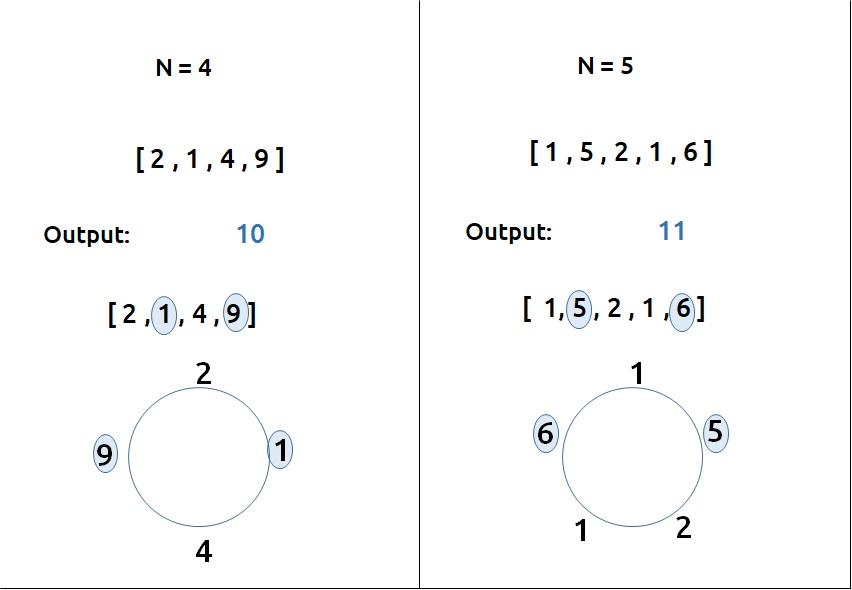
This Problem is the Preveously DPL5 here is the only one Majore Change that is First and Last element is Connected to Each other we can not take both at the Same Time

Thought Process

Basically we Deal with the given array in the 2 different Face

arr1 = arr[1::] (for ans1 in this case we can not consider the 1st element of the given array)

arr2 = arr[:len(arr)-1] (for ans2 in this case we can not consider the last element of the given array)

And Finally we return the max(ans1,ans2)

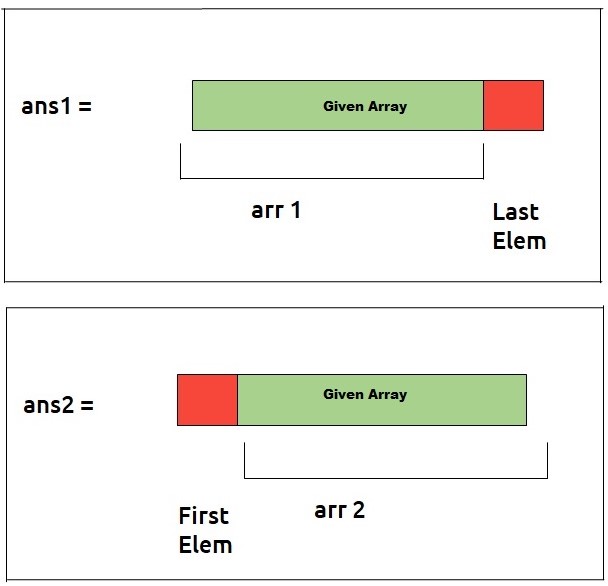
This Problem Entire Implementation is the Same ae Preveously learn in DPL5 for Recursion, Memoization, Tabluation Everything will be same. just we find the all the Solution for the arr1 and arr2 that we discuss in uppper and finally return max(ans1,ans2)

That's why we can not repet the Same Code again that we learned Preveously here we just Implement onlu Space Optimization Approch.

Space Optimization

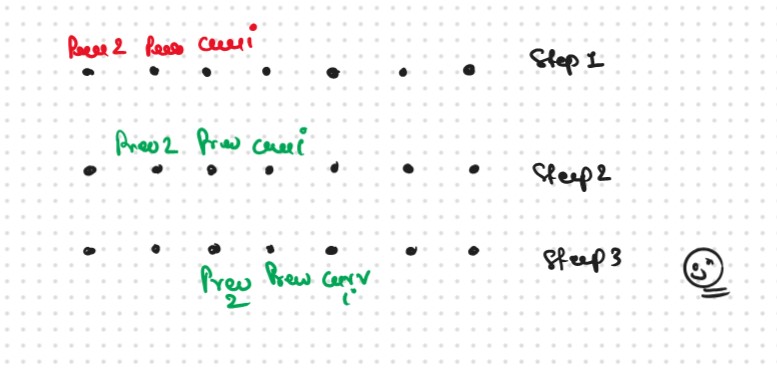
If we closelly Observed if any Tabulation Approch we used the Some Limited Stuff like: ( i,i-1,i-2) for the finding the our ans then definetly here Spaced Optimization is Possible in that types of Problems. Always Remember ( Space Optimization Img From DPL5 )

dp[i], dp[i-1], and dp[i-2]

we see that for any i, we do need only the last two values in the array. So no need to maintain a whole array for the ans

Each iteration’s currIndx and prev become the next iteration’s prev and prev2 respectively.

Therefore after calculating currIndx, if we update prev and prev2 according to the next step, we will always get the answer.

After the iterative loop has ended we can simply return prev as our answer.

Time & Space Complexity

Time Complexity: O(N) + O(N) + O(N) ~ O(N)
Reason: We used a 2 extra array for the ans and We are running a simple iterative loop, two times. Therefore total time complexity will be O(N) + O(N) + O(N) ≈ O(N)
Space Complexity: O(1)
Reason: We are not using any extra space.