JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)
DPL7 Ninja's Training or Vacation Atcoder 2D DP 🔥
A Ninja has an ‘N’ Day training schedule. He has to perform one of these three activities (Running, Fighting Practice, or Learning New Moves) each day. There are merit points associated with performing an activity each day. The same activity can’t be performed on two consecutive days. We need to find the maximum merit points the ninja can attain in N Days.
We are given a 2D Array POINTS of size ‘N*3’ which tells us the merit point of specific activity on that particular day. Our task is to calculate the maximum number of merit points that the ninja can earn.
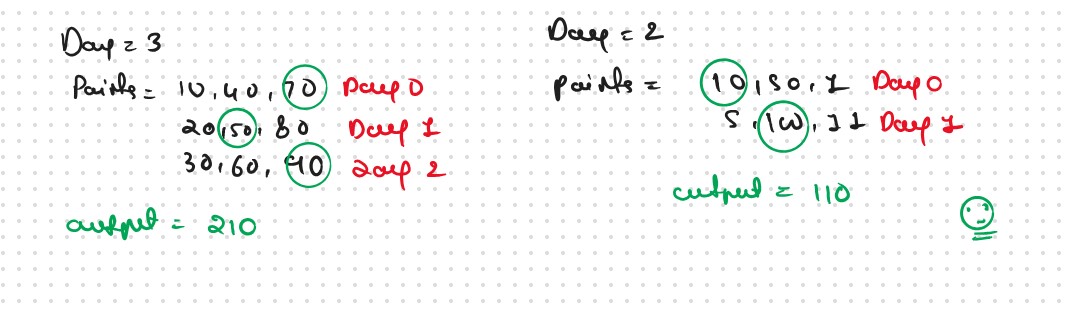
Greedy Approch
Accroding to the Greedy we find the Best Solution on the every Point that is the Defination of the Greedy Algorithm
So if we used the Greedy then our ans may be not correct let's understand
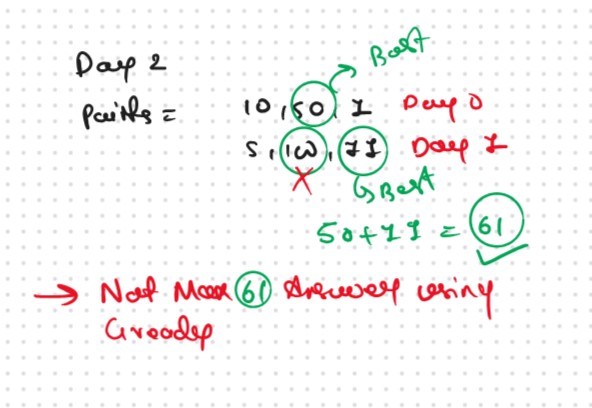 Hence Proved Not Every time Greedy is Correct for the Expected Ans
Hence Proved Not Every time Greedy is Correct for the Expected Ans
As this is a small example we can clearly see that we have a better approach, to consider activity with 10 points on day0 and 100 points on day1. It gives us the total merit points as 110 which is better than the greedy solution.
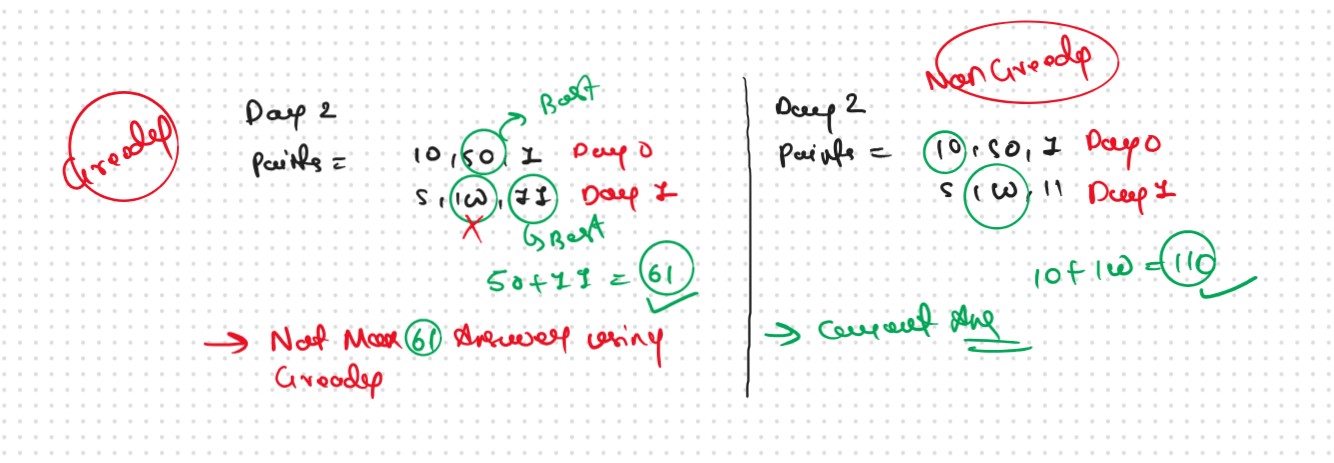
Recursice Approch
Steps to form the recursive solutionStep 1: Express the problem in terms of indexes:
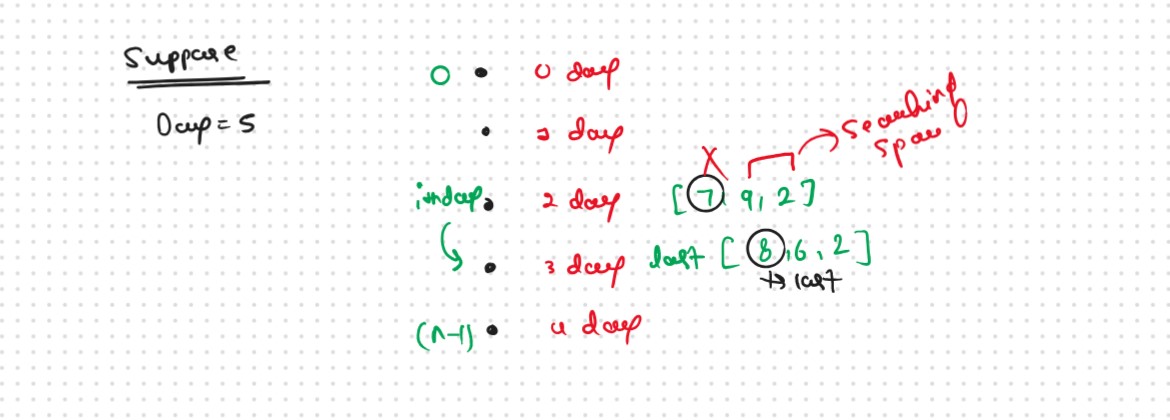
Step 2: Try all the choices to reach the goal. & Try out all possible choices at a given index.
We are writing a top-down recursive function. We start from day n-1 to day 0. Therefore whenever we call the recursive function for the next day we call it for fun(day-1, second parameter). Now let’s discuss the second parameter. The choices we have for a current day depend on the ‘last’ variable. If we are at our base case (day=0), we will have the following choices.

Step 3: Take the maximum of all the choices
Recursion Base Conditions
The base conditions for the recursive Solution
Recursion Tree
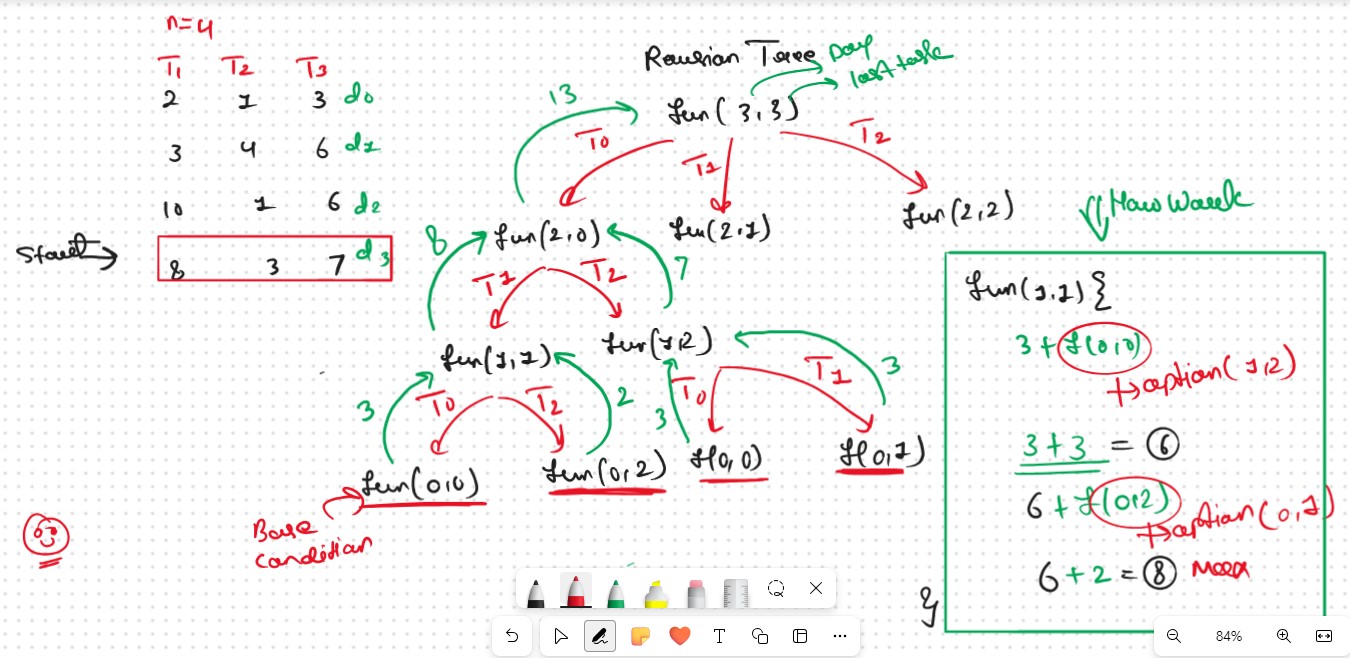
.png)
.png)
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity: O(N*4*3)Reason: Exponential Time we find out the all the Possible Path
Space Complexity: O(N)
Reason: We are using a recursion stack space(O(N))
Memoization Approch
If we observe in the recursion tree, we will observe a many number of overlapping subproblems. Therefore the recursive solution can be memoized for to reduce the time complexity.

Steps to convert Recursive code to memoization solution:
.png)
.png)
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity:O(N*4*3)Reason: There are N*4 states and for every state, we are running a for loop iterating three times.
Space Complexity: O(N) + O(N*4)
Reason: We are using a recursion stack space(O(N)) and a 2D array (again O(N*4)). Therefore total space complexity will be O(N) + O(N) ≈ O(N)
Tabulation Approch
Tabulation is a ‘bottom-up’ approach where we start from the base case and reach the final answer that we want and Memoization is the Top-down Approch.Steps to convert Recursive Solution to Tabulation one.
- First initialize the base condition values. We know that base condition arises when day = 0. Therefore, we can say that the following will be the base conditions
- dp[0][0] = max(points[0][1], points[0][2])
- dp[0][1] = max(points[0][0], points[0][2])
- dp[0][2] = max(points[0][0], points[0][1])
- dp[0][3] = max(points[0][0], points[0][1] and points[0][2])
.png)
.png)
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity: O(N*4*3)Reason:There are three nested loops
Space Complexity: O(N*4)
Reason: We are using an external array of size ‘N*4’’.
Space Optimization
If we closelly Observed if any Tabulation Approch we used the Some Limited Stuff like: ( i,i-1,i-2,i-3) for the finding the our ans then definetly here Spaced Optimization is Possible in that types of Problems. Always Remember
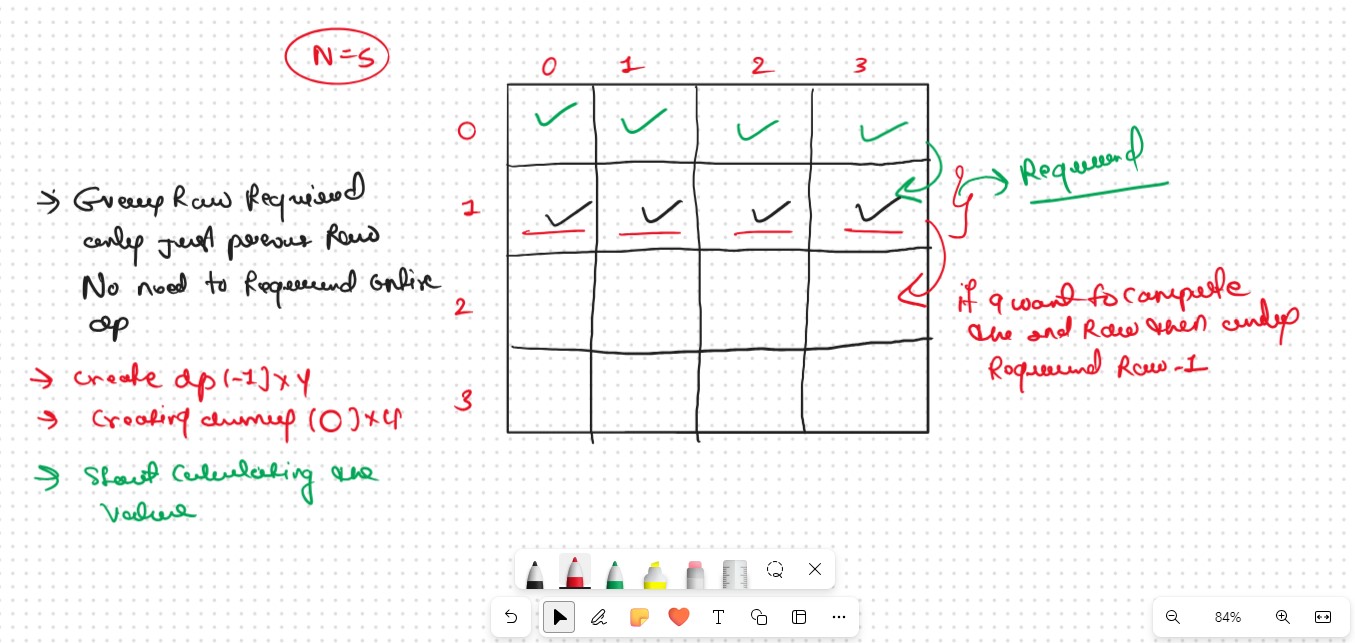
.png)
.png)
Sb Mai He Kru ...
Khud Bhi Kr le Khuch ..... Nalayk
Time & Space Complexity
Time Complexity:O(N*4*3)Reason: There are three nested loops
Space Complexity: O(4)
Reason: We are using an external array of size ‘4’ to store only one row.