JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

L14 Permutations I

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Example 1:
Input: nums = [1,2,3]
OOutput: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Example 2:
nums = [0,1]
Output: [[0,1],[1,0]]

Constraints:
- 1 <= nums.length <= 6
- -10 <= nums[i] <= 10
- All the integers of nums are unique.

Notes

Note: Zoom for Better Understanding

Approch 1

Approach: We have given the nums array, so we will declare an ans vector of vector that will store all the permutations also declare a data structure.

Declare a map and initialize it to zero and call the recursive function

Base condition:

When the data structure’s size is equal to n(size of nums array) then it is a permutation and stores that permutation in our ans, then returns it.

Recursion:

Run a for loop starting from 0 to nums.size() – 1. Check if the frequency of i is unmarked, if it is unmarked then it means it has not been picked and then we pick. And make sure it is marked as picked.

Call the recursion with the parameters to pick the other elements when we come back from the recursion make sure you throw that element out. And unmark that element in the map.

The Total Number of the Permutation of the any Array or String is N! [N: is the len of the Array]

We Manage the DS for Containig the all the Permutation

Again we follow the Pick and Not Pick Concept

One more DS Carray frro marking the Visit element every Time

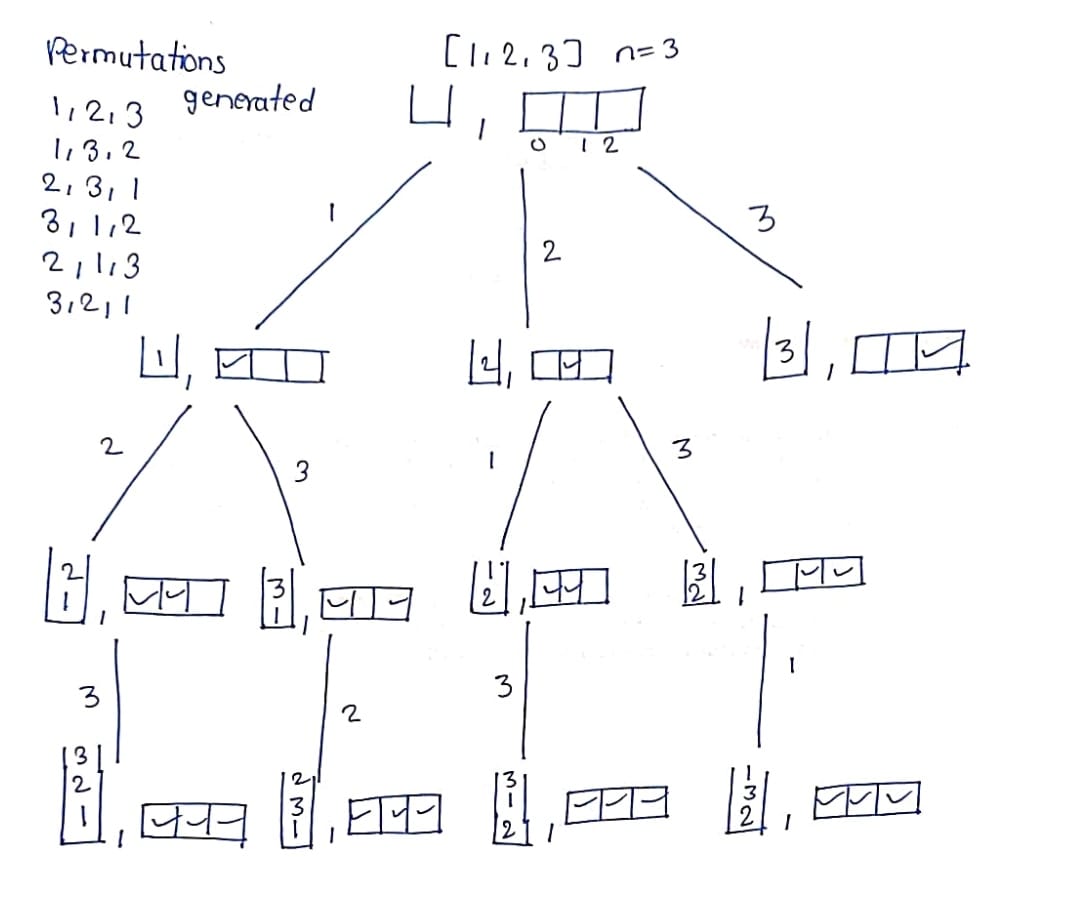
Recursion Tree

Code Zone!

Time Complexity:N! x N
Reason:N! for generating All the Permutation and N: for loop 0 to N every Time Iterate

Space Complexity: O(N) + O(N) + O(N) O(N) for the my ans DS and O(N) for the my visiting Array and O(N) foro the Recursive Stack Space.

Approch 2

As we learn Preveselly we used a extra data structure for the Storing the Visiting Element in this Approch we reduce the Extra Space and we using the Concept of the Swaping Element

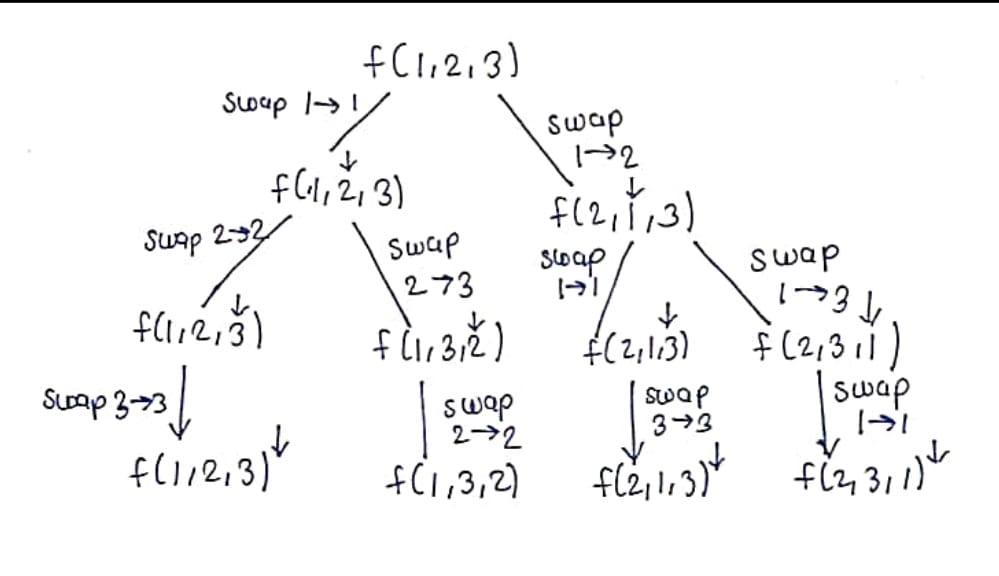
Approach: Using backtracking to solve this.

We have given the nums array, so we will declare an ans vector of vector that will store all the permutations.

Call a recursive function that starts with zero, nums array, and ans vector.

Declare a map and initialize it to zero and call the recursive function

Base condition:

Whenever the index reaches the end take the nums array and put it in ans vector and return.

Recursion:

Go from index to n – 1 and swap once the swap has been done call recursion for the next state. After coming back from the recursion make sure you re-swap it because, for the next element, the swap will not take place.

Recursive Tree:

Code Zone!

Time Complexity:N! x N
Reason:N! for generating All the Permutation and N: for loop 0 to N every Time Iterate

Space Complexity: O(N) + O(N) O(N) for the my ans DS and O(N) foro the Recursive Stack Space.