JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

L16 N-Queens I

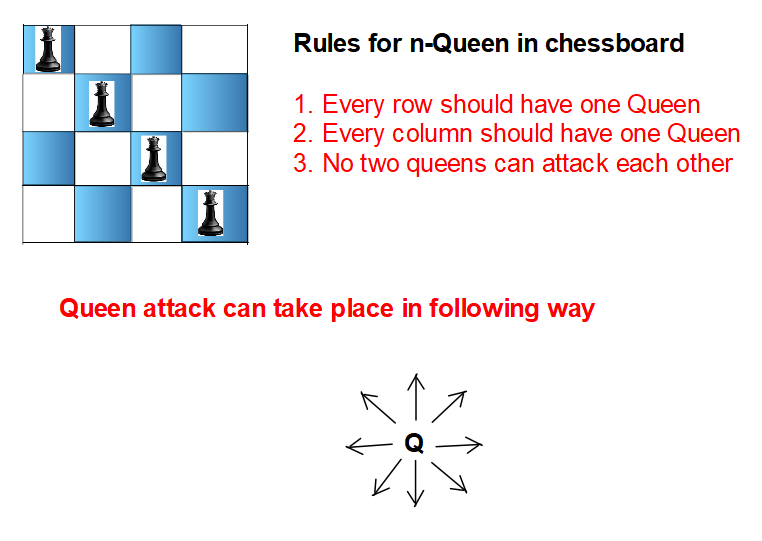
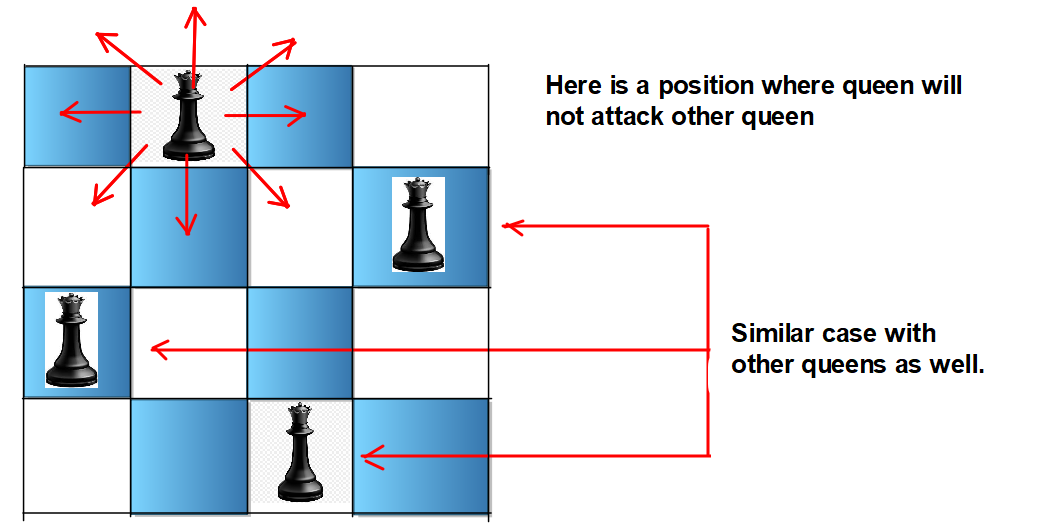
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

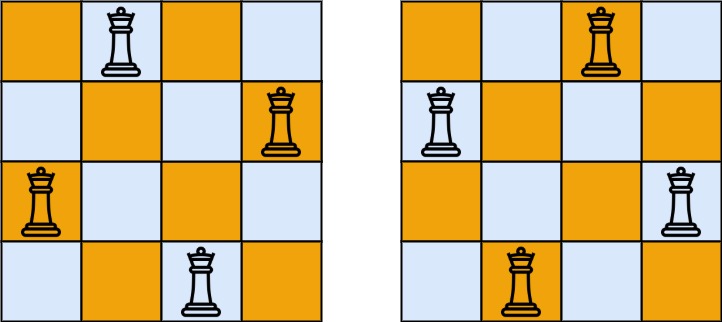
Example 1:
Input: n = 4 Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:
Input: n = 1
Output: [["Q"]]

Constraints:
- 1 <= 9

Notes

Note: Zoom for Better Understanding

Let us first understand how can we place queens in a chessboard so that no attack on either of them can take place.

Intuition: Using the concept of Backtracking, we will place Queen at different positions of the chessboard and find the right arrangement where all the n queens can be placed on the n*n grid.

This is the position where we can see no possible arrangement is found where all queens can be placed since, at the 3rd column, the Queen will be killed at all possible positions of row.

Recursion Tree

Code Zone!

Time Complexity:N! x N
Reason:Exponential in nature, since we are trying out all ways. To be precise it goes as O (N! * N) nearly.

Space Complexity: O(N^2) O(N) for the my ans DS and O(N) for the Recursive Stack Space.

But this is not a Good Approch we used a 3O(N) extra Time try to reduced this time

Using Hashing we removed this extra Time

This is the optimization of the issafe function. In the previous issafe function, we need o(N) for a row, o(N) for the column, and o(N) for the diagonal. Here, we will use hashing to maintain a list to check whether that position can be the right one or not.

For checking Left row elements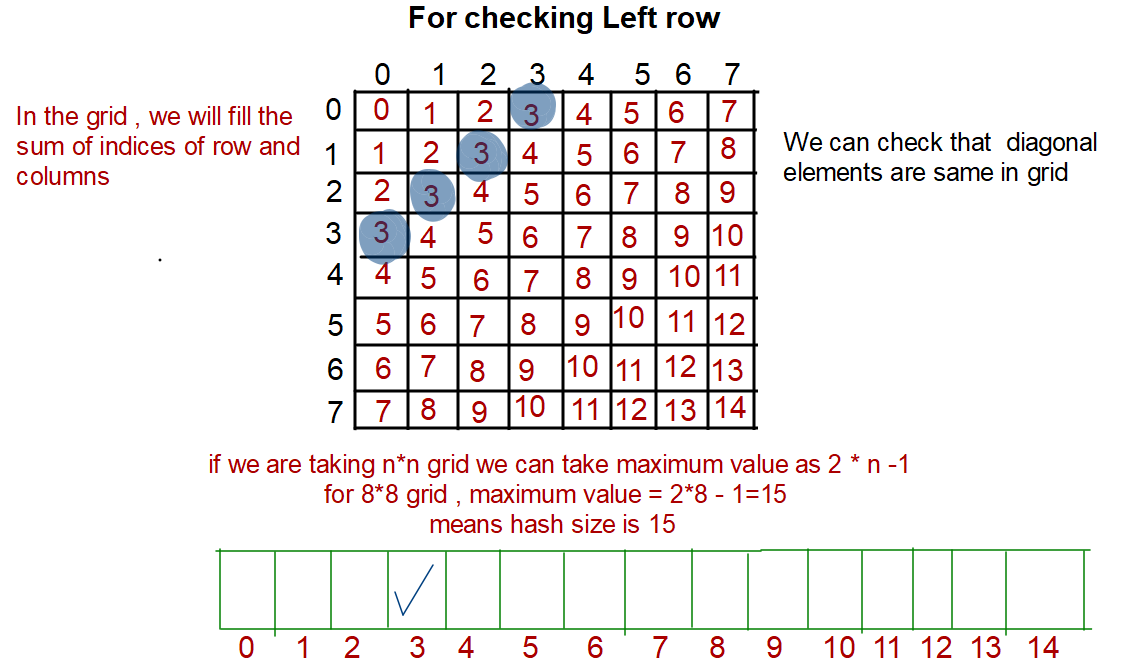 For checking upper diagonal and lower diagonal

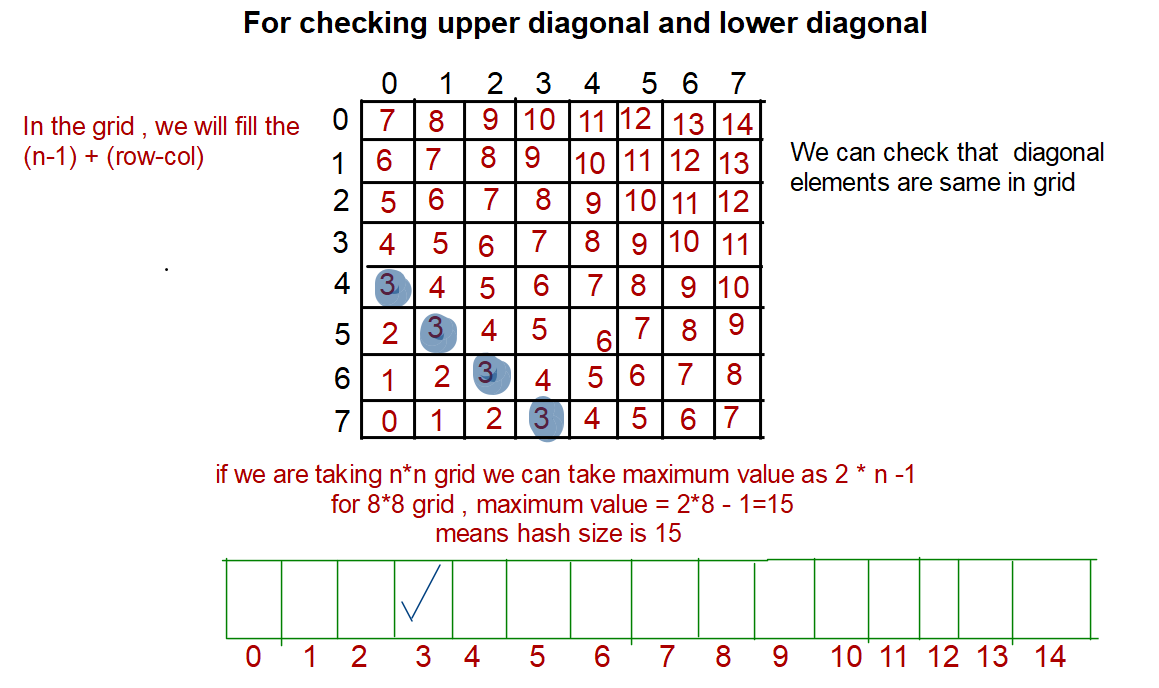
Code Zone!

Time Complexity:N! x N
Reason:Exponential in nature, since we are trying out all ways. To be precise it goes as O (N! * N) nearly.

Space Complexity: O(N) O(N) for the Recursive Stack Space.