JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

L18 Sudoku Solver

Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:

1. Each of the digits 1-9 must occur exactly once in each row.
2. Each of the digits 1-9 must occur exactly once in each column.
3. Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.

Example 1:
Input: board = [["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]]

Output: [["5","3","4","6","7","8","9","1","2"],
["6","7","2","1","9","5","3","4","8"],
["1","9","8","3","4","2","5","6","7"],
["8","5","9","7","6","1","4","2","3"],
["4","2","6","8","5","3","7","9","1"],
["7","1","3","9","2","4","8","5","6"],
["9","6","1","5","3","7","2","8","4"],
["2","8","7","4","1","9","6","3","5"],
["3","4","5","2","8","6","1","7","9"]]
Explanation: The input board is shown above and the only valid solution is shown below:



Constraints:
board.length == 9
board[i].length == 9
board[i][j] is a digit or '.'.
It is guaranteed that the input board has only one solution.

Notes

Note: Zoom for Better Understanding

This is the Standared problem based on the Recursion and Backtracking

Intuition:
Since we have to fill the empty cells with available possible numbers and we can also have multiple solutions, the main intuition is to try every possible way of filling the empty cells. And the more correct way to try all possible solutions is to use recursion. In each call to the recursive function, we just try all the possible numbers for a particular cell and transfer the updated board to the next recursive call.

Let’s see the step by step approach. Our main recursive function(solve()) is going to just do a plain matrix traversal of the sudoku board. When we find an empty cell, we pause and try to put all available numbers(1 – 9) in that particular empty cell.

We need another loop to do that. But wait, we forgot one thing – the board has to satisfy all the conditions, right? So, for that we have another function(isValid()) which will check whether the number we have inserted into that empty cell will not violate any conditions.

If it is violating, we try with the next number. If it is not, we call the same function recursively, but this time with the updated state of the board. Now, as usual it tries to fill the remaining cells in the board in the same way.

Now we’ll come to the returning values. If at any point we cannot insert any numbers from 1 – 9 in a particular cell, it means the current state of the board is wrong and we need to backtrack. An important point to follow is, we need to return false to let the parent function(which is called this function) know that we cannot fill this way. This will serve as a hint to that function, that it needs to try with the next possible number. Refer to the picture below.

If a recursive call returns true, we can assume that we found one possible way of filling and we simply do an early return.

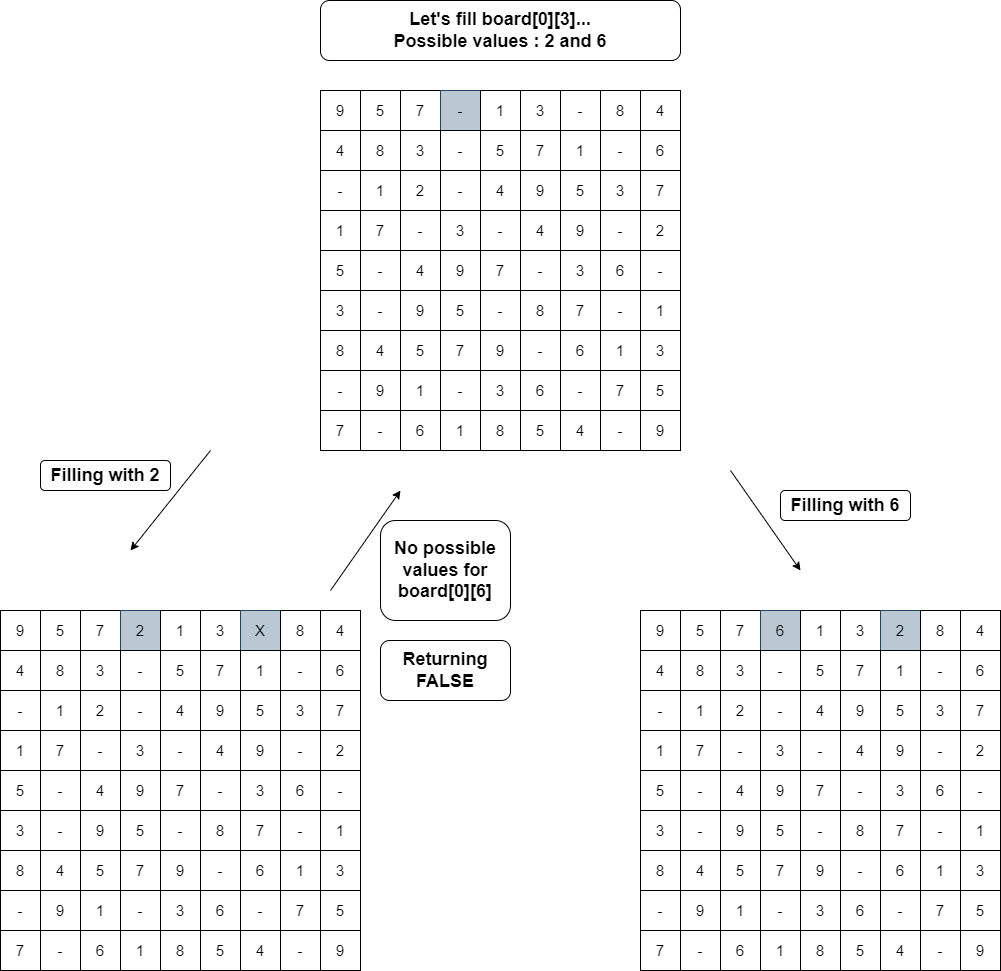
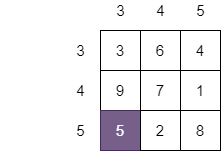
Validating Board

Now, let’s see how we are validating the sudoku board. After determining a number for a cell(at i’th row, j’th col), we try to check the validity. As we know, a valid sudoku needs to satisfy 3 conditions, we can use three loops. But we can do within a single loop itself. Let’s try to understand that.

We loop from 0 to 8 and check the values – board[i][col](1st condition) and board[row][i](2nd condition), whether the number is already included. For the 3rd condition – the expression (3 * (row / 3) + i / 3) evaluates to the row numbers of that 3×3 submatrix and the expression (3 * (col / 3) + i % 3) evaluates to the column numbers.

For eg, if row= 5 and col= 3, the cells visited are

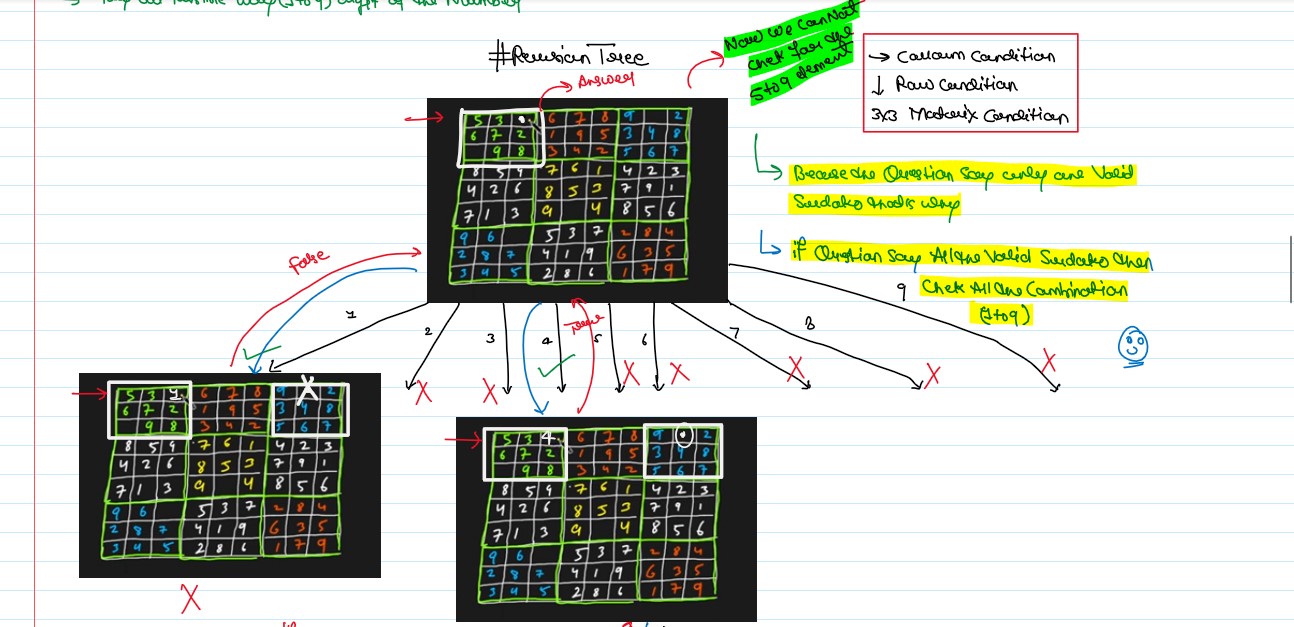
Recursion Tree

Reamaing Tree in the Notes [ Like that we find the Possible Paath ]

Code Zone!

Time Complexity:O(9(n ^ 2)) in the worst case, for each cell in the n2 board, we have 9 possible numbers.
Space Complexity: O(1) + O(N) since we are refilling the given board itself, there is no extra space required, so constant space complexity. O(N) for the Recursive Stack Space.