JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

L21 Permutation Sequence or Kth Permutation Sequence

The set [1, 2, 3, ..., n] contains a total of n! unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for n = 3:
1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"
Given n and k, return the kth permutation sequence.

Example 1:
IInput: n = 3, k = 3
Output: "213"

Example 2:
Input: n = 3, k = 1
Output: "123" Constraints:
- 1 <= n <= 9
- 1 <= k <= n!

Notes

Note: Zoom for Better Understanding

The extreme naive solution is to generate all the possible permutations of the given sequence. This is achieved using recursion and every permutation generated is stored in some other data structure (here we have used a vector). Finally, we sort the data structure in which we have stored all the sequences and return the Kth sequence from it.

Code Zone!

Time Complexity:O(N! * N) +O(N! Log N!)Reason: The recursion takes O(N!) time because we generate every possible permutation and another O(N) time is required to make a deep copy and store every sequence in the data structure. Also, O(N! Log N!) time required to sort the data structure.

Space Complexity: O(N) RReason: Result stored in a vector, we are auxiliary space taken by recursion.

Optimal Approach

Say we have N = 4 and K = 17. Hence the number sequence is {1,2,3,4}.

Intuition:

Since this is a permutation we can assume that there are four positions that need to be filled using the four numbers of the sequence. First, we need to decide which number is to be placed at the first index. Once the number at the first index is decided we have three more positions and three more numbers. Now the problem is shorter. We can repeat the technique that was used previously until all the positions are filled. The technique is explained below.

Approach:

STEP 1:

Mathematically speaking there can be 4 variations while generating the permutation. We can have our permutation starting with either 1 or 2 or 3 or 4. If the first position is already occupied by one number there are three more positions left. The remaining three numbers can be permuted among themselves while filling the 3 positions and will generate 3! = 6 sequences. Hence each block will have 6 permutations adding up to a total of 6*4 = 24 permutations. If we consider the sequences as 0-based and in the sorted form we observe:-

The 0th – 5th permutation will start with 1

The 6th – 11th permutation will start with 2

The 12th – 17th permutation will start with 3

The 18th – 23rd permutation will start with 4.

(For better understanding refer to the picture below.)


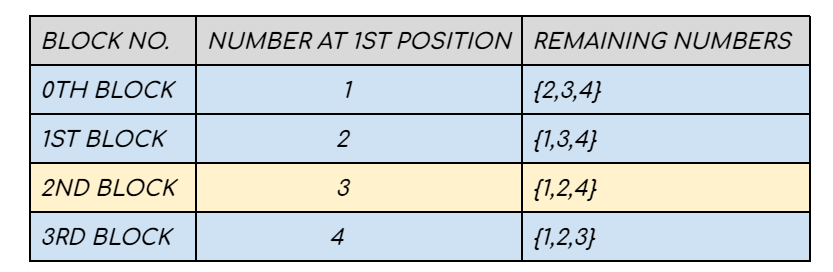
We make K = 17-1 considering 0-based indexing. Since each of the four blocks illustrated above comprises 6 permutations, therefore, the 16th permutation will lie in (16 / 6 ) = 2nd block, and our answer is the (16 % 6) = 4th sequence from the 2nd block. Therefore 3 occupies the first position of the sequence and K = 4.


STEP 2:

Our new search space comprises three elements {1,2,4} where K = 4 . Using the previous technique we can consider the second position to be occupied can be any one of these 3 numbers. Again one block can start with 1, another can start with 2 and the last one can start with 4 . Since one position is fixed, the remaining two numbers of each block can form 2! = 2 sequences. In sorted order :

The 0th – 1st sequence starts with 1

The 2nd – 3rd sequence starts with 2

The 4th – 5th sequence starts with 4

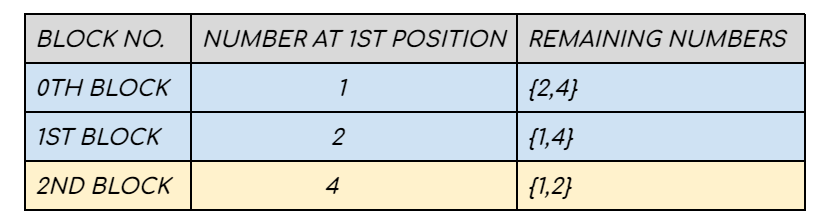
The 4th permutation will lie in (4/2) = 2nd block and our answer is the 4%2 = 0th sequence from the 2nd block. Therefore 4 occupies the second position and K = 0.


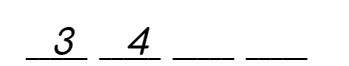
STEP 3:

The new search space will have two elements {1 ,2} and K = 0. One block starts with 1 and the other block starts with 2. The other remaining number can form only one 1! = 1 sequence. In sorted form –

The 0th sequence starts with 1

The 1st sequence. starts with 2

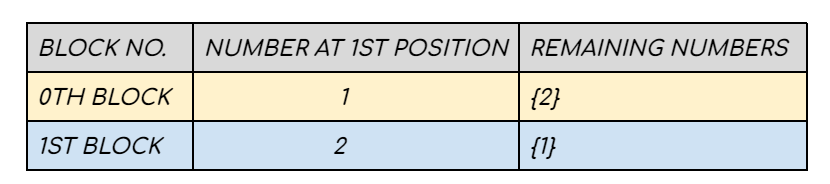
The 0th permutation will lie in the (0/1) = 0th block and our answer is the 0%1 = 0th sequence from the 0th block. Therefore 1 occupies the 3rd position and K = 0.


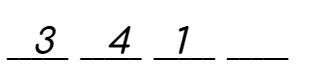
STEP 4:

Now the only block has 2 in the first position and no remaining number is present.


This is the point where we place 2 in the last position and stop.

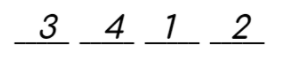The final answer is 3412.

Code Zone!

Time Complexity:O(N) * O(N) = O(N^2) Reason: We are placing N numbers in N positions. This will take O(N) time. For every number, we are reducing the search space by removing the element already placed in the previous step. This takes another O(N) time.

Space Complexity: O(N) Reason: We are storing the numbers in a data structure(here vector).