JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

L22 Rat in a Maze Problem - I

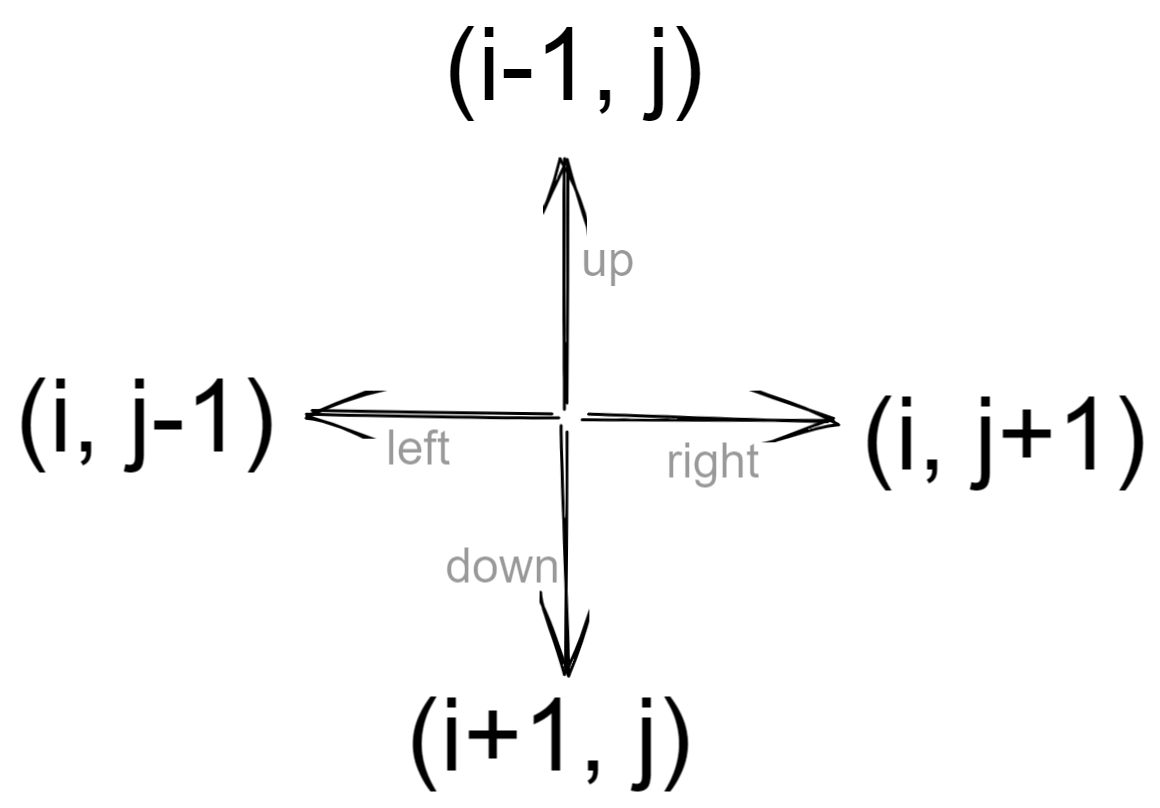
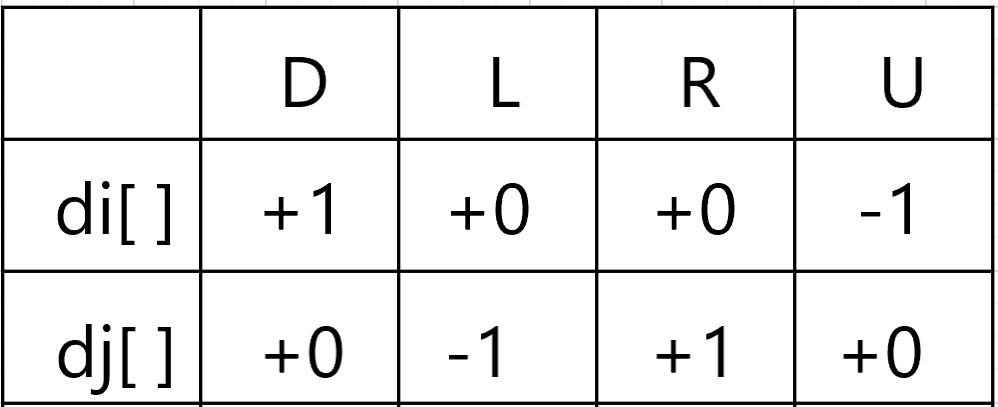
Consider a rat placed at (0, 0) in a square matrix of order N * N. It has to reach the destination at (N - 1, N - 1). Find all possible paths that the rat can take to reach from source to destination. The directions in which the rat can move are 'U'(up), 'D'(down), 'L' (left), 'R' (right). Value 0 at a cell in the matrix represents that it is blocked and rat cannot move to it while value 1 at a cell in the matrix represents that rat can be travel through it.
Note: In a path, no cell can be visited more than one time. If the source cell is 0, the rat cannot move to any other cell.

Example 1:
Input: N = 4
m[][] = {{1, 0, 0, 0},
{1, 1, 0, 1},
{1, 1, 0, 0},
{0, 1, 1, 1}}

Output:
DDRDRR DRDDRR

Explanation: The rat can reach the destination at (3, 3) from (0, 0) by two paths - DRDDRR and DDRDRR, when printed in sorted order we get DDRDRR DRDDRR.

Example 2:
Input: N = 2
m[][] = {{1, 0},
{1, 0}}
Output:
-1

Explanation: No path exists and destination cell is blocked.

Constraints:
- 1 <= s.length <=16
- s contains only lowercase English letters.

Notes

Note: Zoom for Better Understanding

The best way to solve such problems is using recursion.

Approach:

Start at the source(0,0) with an empty string and try every possible path i.e upwards(U), downwards(D), leftwards(L) and rightwards(R).

As the answer should be in lexicographical order so it’s better to try the directions in lexicographical order i.e (D,L,R,U)

Declare a 2D-array named visited because the question states that a single cell should be included only once in the path,so it’s important to keep track of the visited cells in a particular path.

If a cell is in path, mark it in the visited array.

Also keep a check of the “out of bound” conditions while going in a particular direction in the matrix.

Whenever you reach the destination(n,n) it’s very important to get back as shown in the recursion tree.

While getting back, keep on unmarking the visited array for the respective direction.Also check whether there is a different path possible while getting back and if yes, then mark that cell in the visited array.

Recursion Tree

Code Zone!

Time Complexity:O(4^(m*n))because on every cell we need to try 4 different directions.

Space Complexity:O(m*n) Reason: Maximum Depth of the recursion tree(auxiliary space).

But, writing an individual code for every direction is a lengthy process therefore we truncate the 4 “if statements” into a single for loop using the following approach.

Code Zone!

Time Complexity:O(4^(m*n))because on every cell we need to try 4 different directions.

Space Complexity:O(m*n) Reason: Maximum Depth of the recursion tree(auxiliary space).