JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

L9 Combination Sum II

Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.

Each number in candidates may only be used once in the combination.

Note: The solution set must not contain duplicate combinations.

Example 1:
candidates = [10,1,2,7,6,1,5], target = 8
Output: [ [1,1,6], [1,2,5], [1,7], [2,6] ]
Example 2:
Input: candidates = [2,5,2,1,2], target = 5
Output: [ [1,2,2], [5] ]
Constraints:
- 1 <= candidates.length <= 100
- 1 <= candidates[i] <= 50
- 1 <= target <= 30

Notes

Note: Zoom for Better Understanding

Only a Single Chaneg from the L8 Combination Sum I

And Remaining Code Will be Smae becouse here we used the Each number in candidates may only be used once in the combination.

Code Zone!

Python Code

Java Code

C++ Code

Sb Mai He Kru ...

Khud Bhi Kr le Khuch ..... Nalayk

Time Complexity:O(2^n*k) * log(t)
Space Complexity:O(k*x)
Reason: if we have x combinations then space will be x*k where k is the average length of the combination.

But Interviewer Not Happy with Thes Solution and he Asked I Don't Want to the Extra Time Complexcity: log(t)

Before starting the recursive call make sure to sort the elements because the ans should contain the combinations in sorted order and should not be repeated.

Initially, We start with the index 0, At index 0 we have n – 1 way to pick the first element of our subsequence.

Check if the current index value can be added to our ds. If yes add it to the ds and move the index by 1. while moving the index skip the consecutive repeated elements because they will form duplicate sequences.

Reduce the target by arr[i],call the recursive call for f(idx + 1,target – 1,ds,ans) after the call make sure to pop the element from the ds.(By seeing the example recursive You will understand).

if(arr[i] > target) then terminate the recursive call because there is no use to check as the array is sorted in the next recursive call the index will be moving by 1 all the elements to its right will be in increasing order.

Base Condition: Whenever the target value is zero add the ds to the ans return.
Representation of Recursive call for the example given below:

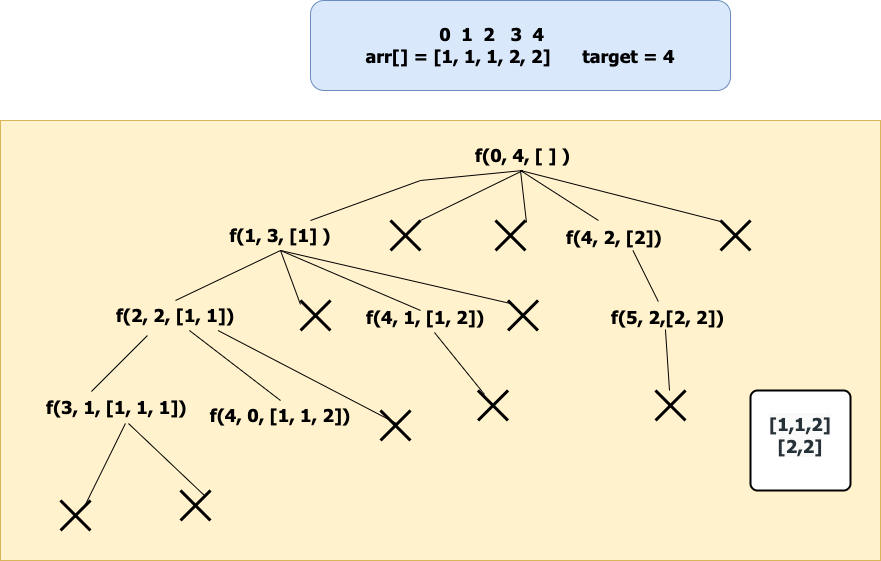
If we observe the recursive call for f(2,2,[1,1]) when it is returning the ds doesn’t include 1 so make sure to remove it from ds after the call. Backtracking

Recursive Tree