JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

SQP13 Rotting Oranges

You are given an m x n grid where each cell can have one of three values:

0 representing an empty cell,

1 representing a fresh orange, or

2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

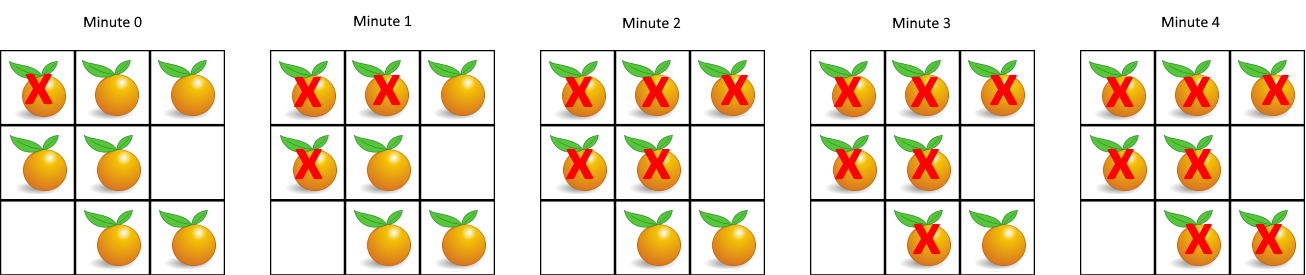
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Explanation:
The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 2:
Input: grid = [[0,2]]
Output: 0
Explanation:
Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 10
- grid[i][j] is 0, 1, or 2.

Notes

Note: Zoom for Better Understanding

Thought Process

This Question Based on the Graph But we Implement in the Stack and Queue

In this Problem we have a M X N grid and we have a some Instruction.

0 -> Represent the Empty Cell

1 -> Represent the Fresh Orange Cell

2 -> Represent the rotten Orange Cell

Here we used the concept of the BFS and we required the Queue Data Structure

Basically we first count the fresh,rotten and empty cell in the Matrix

Maintain the Queue Data Structure

Now put the Rottern oranges row-> Index and coll-> Index Pair (row,coll)

After Storing the Rotten Oranges start the Iteration on that Rotten Oranges in the Given Direction

After Complete the one Full Iteration of the existance Rotten Oranges into the Queue Increase the our Minute + 1

The algorithm steps are as follows:

For BFS traversal, we need a queue data structure and a visited array. Create a replica of the given array, i.e., create another array of the same size and call it a visited array. We can use the same matrix, but we will avoid alteration of the original data.

The pairs of cell number and initial time, i.e., <(row, column)>, time> will be pushed in the queue and marked as visited (represents rotten) in the visited array. For example, ((2,0), 0) represents cell (2, 0) and initial time 0.

While BFS traversal, pop out an element from the queue and travel to all its neighbours. In a graph, we store the list of neighbours in an adjacency list but here we know the neighbours are in 4 directions.

We go in all 4 directions and check for valid unvisited fresh orange neighbours. To travel 4 directions we will use nested loops, you can find the implementation details in the code.

BFS function call will make sure that it starts the BFS call from each rotten orange cell, and rotten all the valid fresh orange neighbours and puts them in the queue with an increase in time by 1 unit. Make sure to mark it as rotten in the visited array.

Pop-out another rotten orange from the queue and repeat the same steps until the queue becomes empty.

Add a counter variable to store the maximum time and return it. If any of the fresh was not rotten in the visited array then return -1.

Consider the following example to understand how BFS traverses the cells and rotten the oranges accordingly.

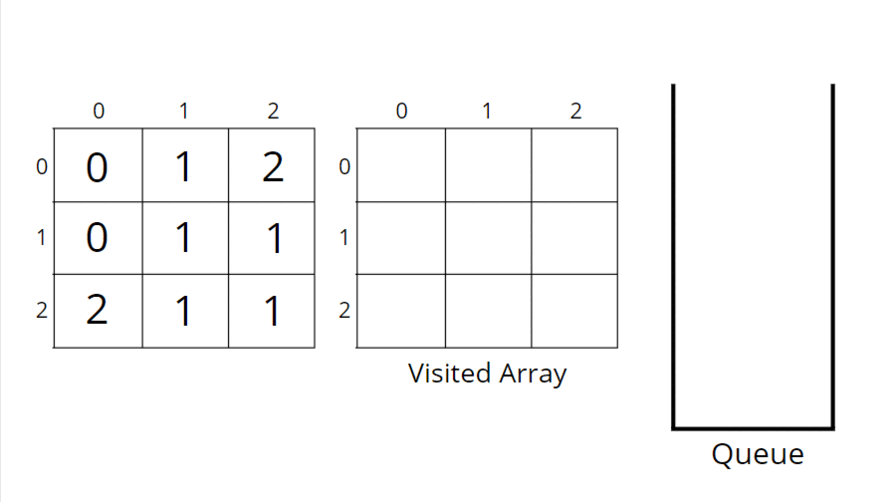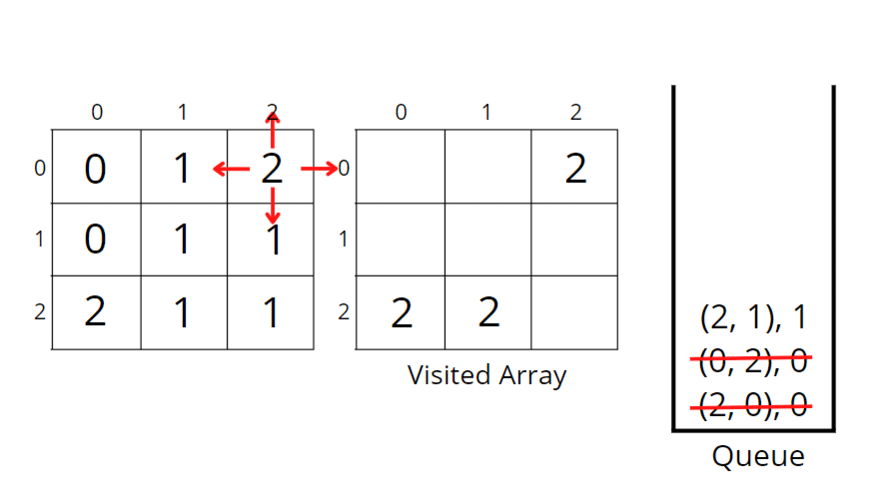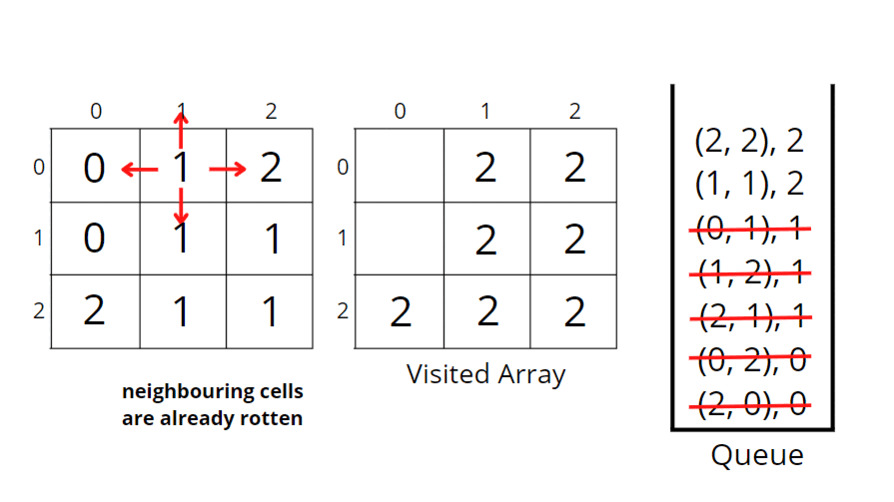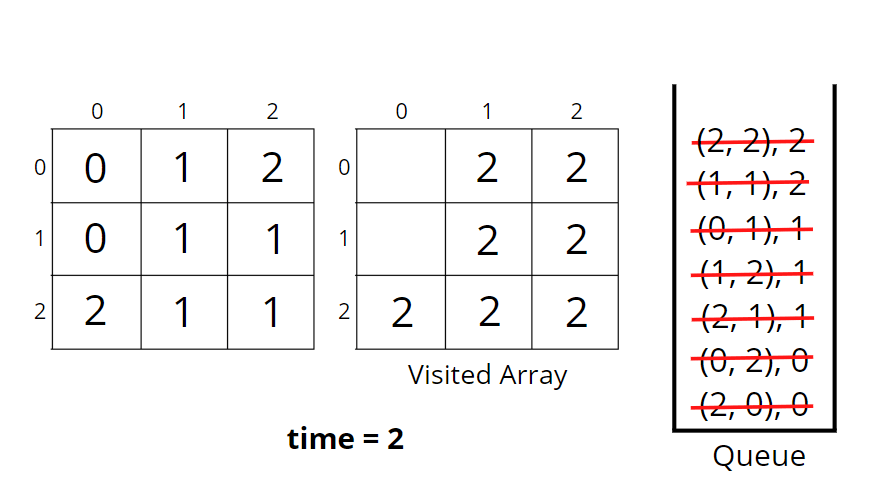
How do set boundaries for 4 directions?
The 4 neighbours will have the following indexes:
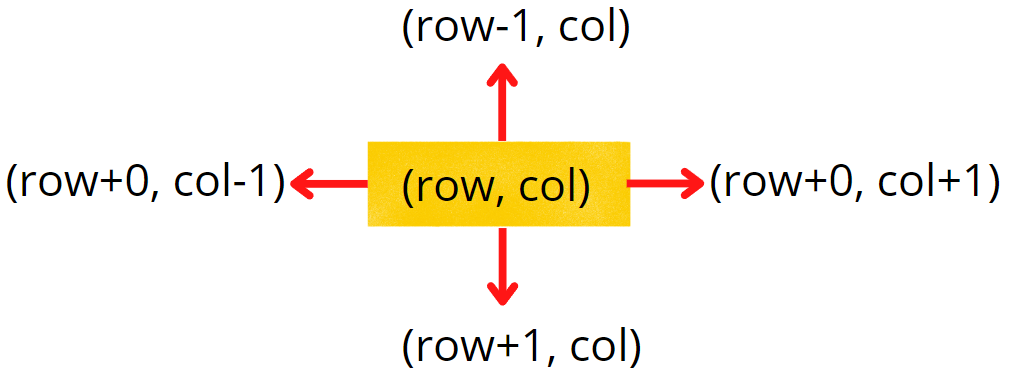
Now, either we can apply 4 conditions or follow the following method.

From the above image, it is clear that the delta change in a row is -1, +0, +1, +0. Similarly, the delta change in column is 0, +1, +0, -1. So we can apply the same logic to find the neighbours of a particular pixel (row, column).

Code Zone!

Time Complexity:O(NxM + NxMx4) ~ O(N x M) For the worst case, all of the cells will have fresh oranges, so the BFS function will be called for (N x M) nodes and for every node, we are traversing for 4 neighbours, it will take O(N x M x 4) time.

Space Complexity:O(N x M), O(N x M) for copied input array and recursive stack space takes up N x M locations at max.