JB TAK FODEGA NHI .... TB TK CHODEGA NHI .... (MAANG)

SQP9 Implementation LRU Cache

Design a data structure that follows the constraints of a Least Recently Used (LRU) cache.

Implement the LRUCache class:

  • LRUCache(int capacity) Initialize the LRU cache with positive size capacity.
  • int get(int key) Return the value of the key if the key exists, otherwise return -1.
  • void put(int key, int value) Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.
    • The functions get and put must each run in O(1) average time complexity.

    Example 1:
    Input:["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
    [[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
    Output: [null, null, null, 1, null, -1, null, -1, 3, 4]
    Explanation:
    LRUCache lRUCache = new LRUCache(2);
    lRUCache.put(1, 1); // cache is {1=1}
    lRUCache.put(2, 2); // cache is {1=1, 2=2}
    lRUCache.get(1); // return 1
    lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
    lRUCache.get(2); // returns -1 (not found)
    lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
    lRUCache.get(1); // return -1 (not found)
    lRUCache.get(3); // return 3
    lRUCache.get(4); // return 4

    Constraints:
    - 1 <= capacity <= 3000
    - 0 <= key <= 104
    - 0 <= value <= 105
    - At most 2 * 105 calls will be made to get and put.

    Notes

    Note: Zoom for Better Understanding



    Approch

    Basically we Degine the Data Structure that follow the Properties of the LRU in this problem we have a tuple of the finction

  • get()
  • put()

    • get function return the value of the particular key, if the key is not present into the ds retuirn -1 get(key)

    put function used for the we gives the key and value and we put into the cache data structure put(key,val)

  • if the capacity of the data structure s filled then return -1

    • remove the least recent used guy and then we will Insert the our New pair

    Implementation and Dry run into the Notes check out

    Code Zone!

    Before Loking the Code...
    Try by Your Self ...

    Python Code
    C++ Code
    Java Code
    Sb Mai He Kru ...

    Khud Bhi Kr le Khuch ..... Nalayk


    Time Complexity:O(N) Linear Iteration
    Space Complexity:O(N) O(N) Stack Space.


    Interviewer Not Happy with these Solution Becouse we used a Extra Space O(N) time to optimized the Approch

    Optimized Approch

    Prerequisite: Should have knowledge on the topics Hashmaps & DLL(Doubly Linked List)

    While inserting the {key,val} pair into the DDL make sure that we are inserting it from the back tail to head.
    The cache will tell us when the {key, value} pair is used/inserted.
    Approach:
    Size = 3
    put(1,10)
    put(3,15)
    put(2,12)
    get(3)
    put(4,25)
    Create a DLL and hashmap


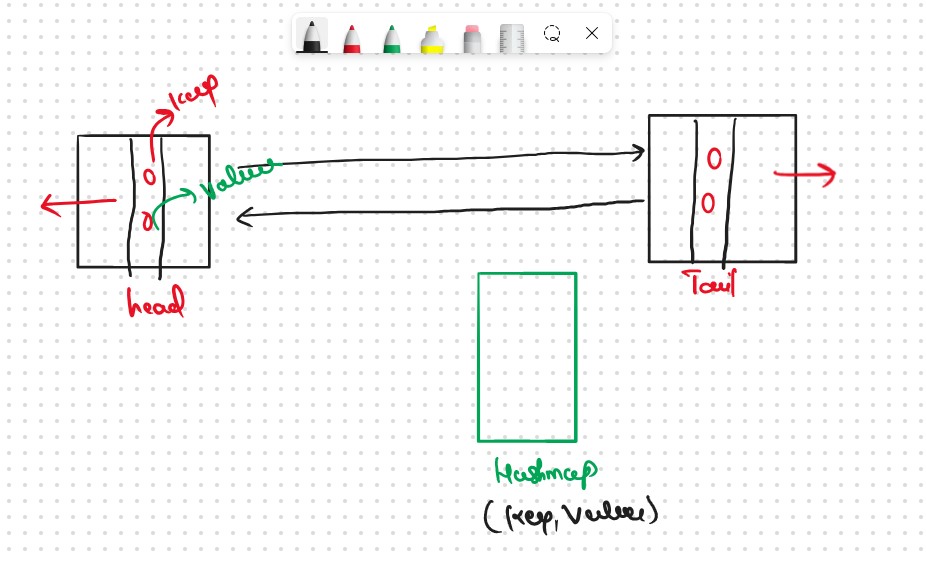
    While inserting the {key,val}pair consider the following

  • Check if the {key,val} pair is already present in Cache.
  • Check for the capacity. if the Cache size == capacity then while inserting the new pair remove the LRU and insert the new pair right after the head.while removing the node make sure to remove the {value, node} pair from the cache
    • .
  • If the key is not present in the Cache then return -1;
    • Query 1: put(1,10)
    Initialling Cache is empty so (n = 0) and (1,10) are not present in the Cache. It is a new element so we should insert it into the Cache.
    Since n < capacity(0 < 3), so we can insert the pair.
    Insert the pair({1,10}) right after the head.And store the {key,address of the node x} in the Cache.


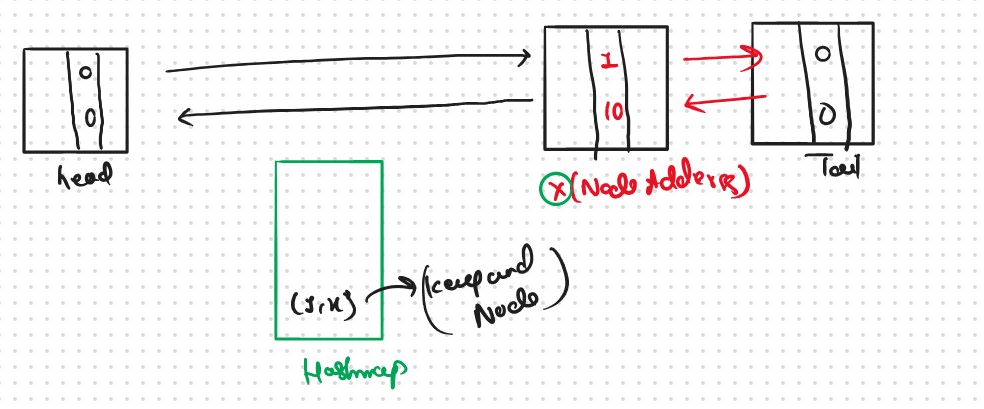
    Query 2: put(3,15)
    Repeat the same process.
    (3,15) is not present in the Cache and the size of the Cache (n = 1) is less than capacity 3.
    Insert the pair(3,10) right after the head and store the address of that node in the Cache with its key value.


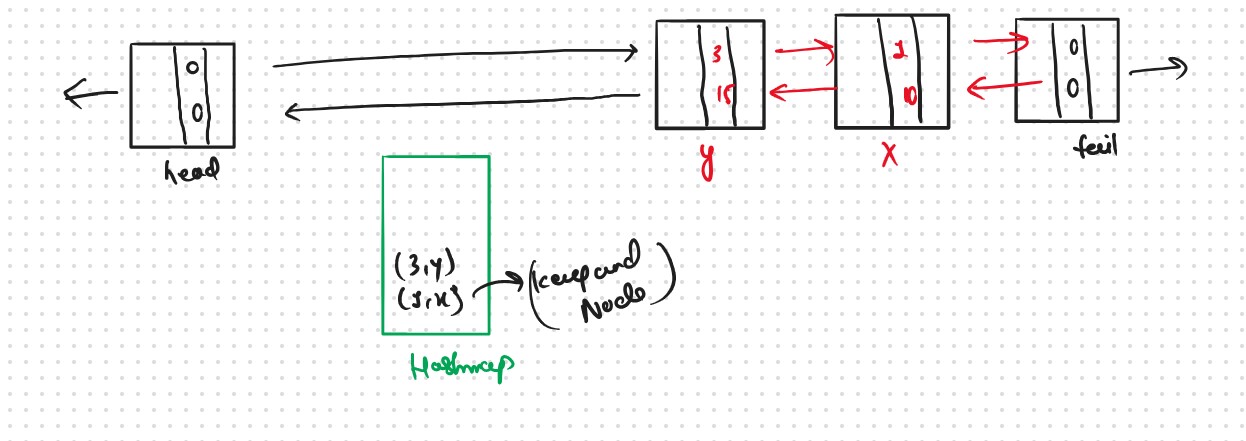
    Query 3: put(2,12)
    Repeat again. check if (2,12) Is present in the Cache.
    No, it’s not present in the cache so now check for the size Cache size is 2 < capacity(3).so insert the pair right after the head.


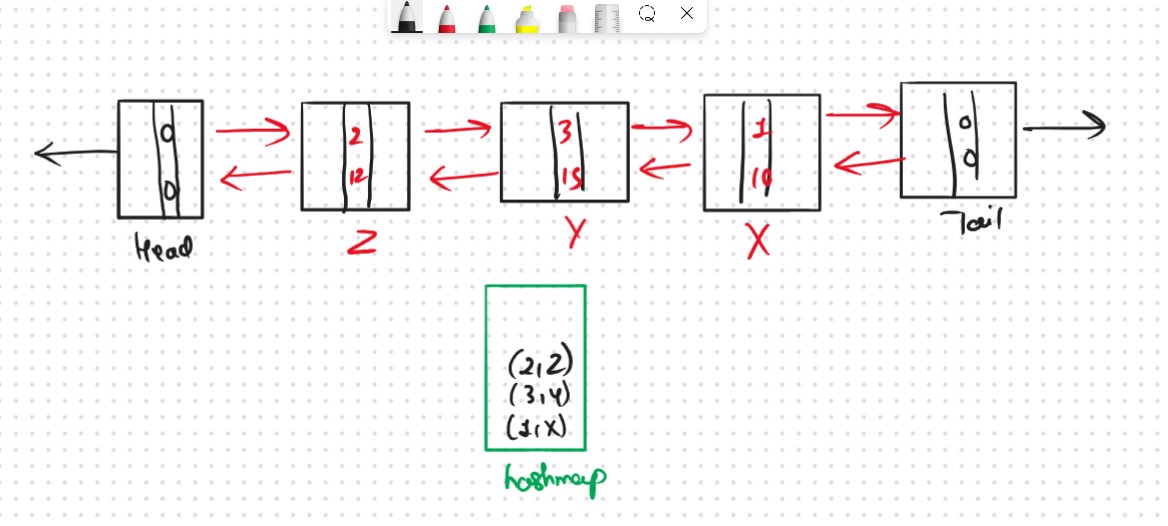
    Query 4: get(3)
    Check if the value is present in the cache. Yes, 3 is present in the cache so take the address of the node(Y) and output the value which is present in that node.
    Now the most recently used should be changed because the flow is from head(most recent) to tail(least recent).
    Delete the node and add that node right after the head. Since the node is moved to a new address update the address of the key in the cache.


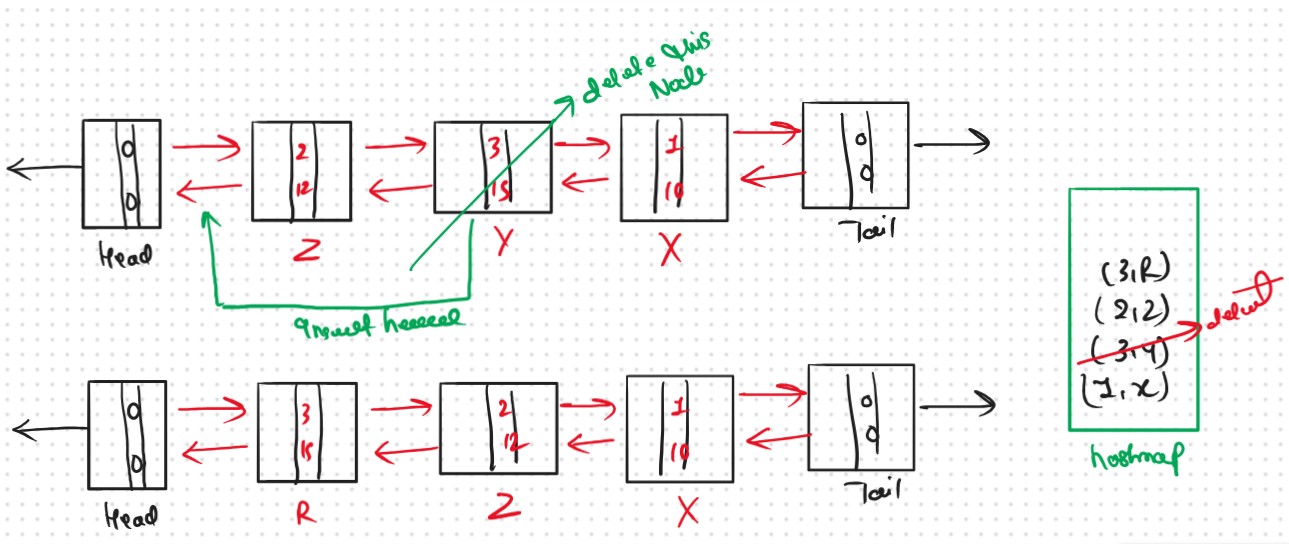
    Query 5: put(4,25)
    Check for the size of the cache n = 3 which is equal to capacity so we have to remove the LRU which is present right before the tail.
    Before removing the node delete the pair{key, node} of that node present in the cache.


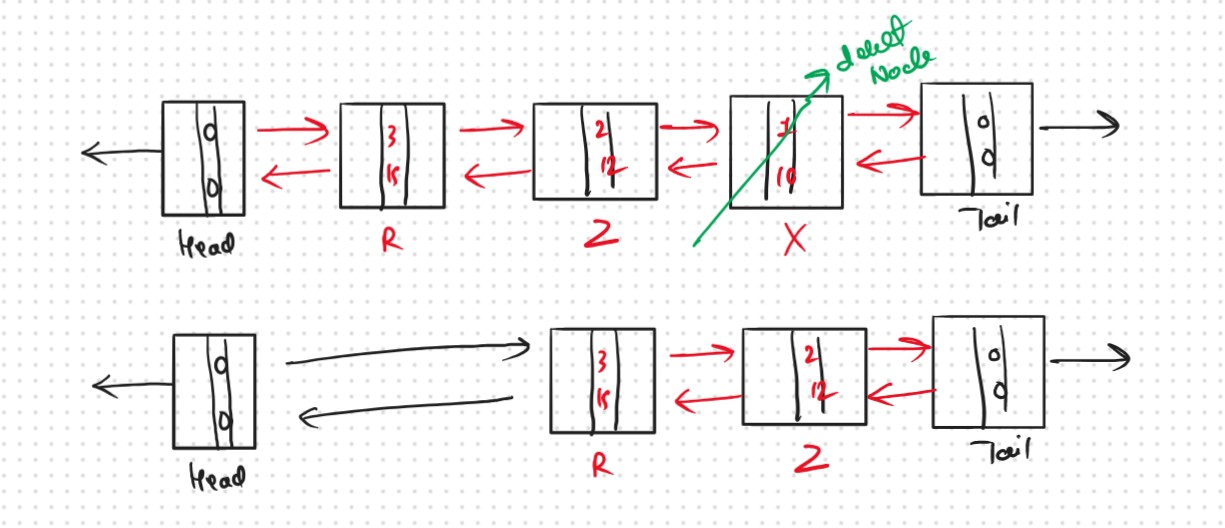
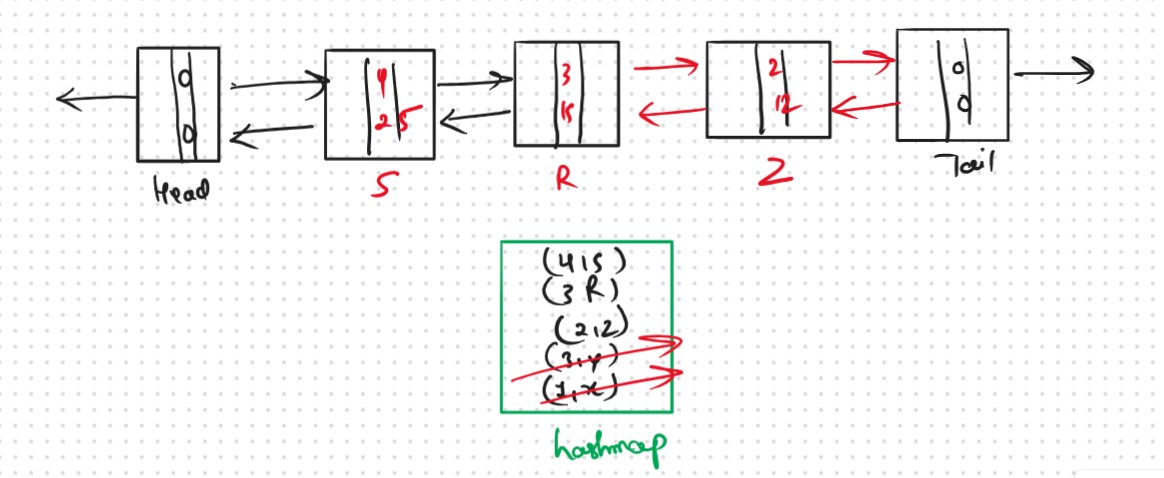
    Now the size of the cache will be 2 now we have space to insert the pair(4,25).
    Take (4,25) right after the head and take the address of the node(s) and insert it into the cache.



    Code Zone!

    Optimized Python Code
    Optimized C++ Code
    Optimized Java Code
    Sb Mai He Kru ...

    Khud Bhi Kr le Khuch ..... Nalayk


    Time Complexity:O(N) Linear Iteration
    Space Complexity:O(1) Becouse we can not used a any further data structure for our answer.


    Color
    Background
    Interview Docs File "All the Best" Team @DSAwithPrinceSingh

    ~ It's All About Consistency📈 Dedication🎯 HardWork💪 Happy Coding❤️ ~